题目内容
4.半径为4的正n边形边心距为2$\sqrt{3}$,则此正n边形的边数为6.分析 由三角函数求出∠DAO=60°,得出∠AOD=30°,求出中心角∠AOB=60°,即可得出答案.
解答 解:如图所示AB为正n边形的边长,OA为半径,OD为边心距,
∵半径为4的正n边形边心距为2$\sqrt{3}$,
∴sin∠DAO=$\frac{DO}{AO}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠DAO=60°,
∴∠AOD=30°,
∴∠AOB=60°,
∴n=$\frac{360°}{60°}$=6.
故答案为:6.
点评 此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠AOB=60°是解题关键.

练习册系列答案
相关题目
 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.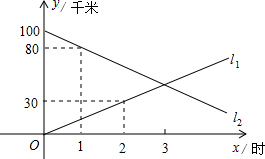 A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.
A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地出发,相向而行.假设他们都保持匀速行驶,则他们各自离A地的距离y(千米)都是骑车时间x(时)的一次函数,1小时后乙距离A地80千米;2时后甲距离A地30千米.
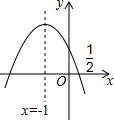 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)
如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)