题目内容
9. 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
分析 过点A作AE⊥CD于E,设CE=xm,解直角三角形求出AE,解直角三角形求出BM、DM,即可得出关于x的方程,求出方程的解即可.
解答 解:过点A作AE⊥CD于E,
则四边形ABDE是矩形,
设CE=xm,在Rt△AEC中,∠AEC=90°,∠CAE=30°,
所以AE=$\frac{CE}{tan30°}$=$\sqrt{3}$xm,
在Rt△CDM中,CD=CE+DE=CE+AB=(x+6)m,
DM=$\frac{CD}{tan60°}$=$\frac{\sqrt{3}(x+6)}{3}$m,
在Rt△ABM中,BM=$\frac{AB}{tan37°}$=$\frac{6}{tan37°}$m,
AE=BD,
所以$\sqrt{3}$x=$\frac{6}{tan37°}$+$\frac{\sqrt{3}(x+6)}{3}$,
解得:x=$\frac{3\sqrt{3}}{tan37°}$+3,
∴CD=CE+ED=$\frac{3\sqrt{3}}{tan37°}$+9≈15.90(m),
答:通信塔CD的高度约为15.90m.
点评 本题考查了解直角三角形,能通过解直角三角形求出AE、BM的长度是解此题的关键.

练习册系列答案
相关题目
20.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系是
( )
( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
17.在|-2|,-2,(-2)5,-|-2|这五个数中,负数共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.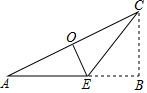 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
7.为测量某特种车辆的性能,研究制定了行驶指数P,P=K+1000,而K的大小与平均速度v(km/h)和行驶路程s(km)有关(不考虑其他因素),K由两部分的和组成,一部分与v2成正比,另一部分与sv成正比.在实验中得到了表格中的数据:
(1)用含v和s的式子表示P;
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
| 速度v | 40 | 60 |
| 路程s | 40 | 70 |
| 指数P | 1000 | 1600 |
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
 填空,完成下列说理过程:
填空,完成下列说理过程: 在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3.
在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3. 如图,AC与BD相交于E,且AC=BD
如图,AC与BD相交于E,且AC=BD