题目内容
9. 在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3.
在△ABC中,AD⊥BC,∠B=45°,∠C=30°,CD=3.(1)求AB长;
(2)求△ABC面积.
分析 (1)先根据直角三角形的性质求出AD的长,再根据直角三角形的性质求出AB的长;
(2)由等腰直角三角形的性质即可得出AD=BD,可求BC,再根据三角形的面积公式可得出结论.
解答 解:(1)∵AD⊥BC,∠C=30°,CD=3,
∴AD=$\frac{\sqrt{3}}{3}$CD=$\sqrt{3}$,
∵∠B=45°,
∴AB=$\sqrt{2}$AD=$\sqrt{6}$;
(2)AD=BD=$\sqrt{3}$,
△ABC面积=($\sqrt{3}$+3)×$\sqrt{3}$÷2=$\frac{3+3\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,直角三角形的性质,等腰直角三角形的性质,三角形的面积,求出AD的长是解答此题的关键,.

练习册系列答案
相关题目
14.某通信公司自2016年2月1日起实行新的4G飞享套餐,部分套餐资费标准如下:
小明每月大约使用国内数据流量200MB,国内主叫200分钟,若想使每月付费最少,则他应预定的套餐是( )
| 套餐 类型 | 月费 (元/月) | 套餐内包含内容 | 套餐外资费 | ||
| 国内数据流量(MB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
| 套餐1 | 18 | 100 | 0 | 0.29 元/MB | 0.19 元/分钟 |
| 套餐2 | 28 | 100 | 50 | ||
| 套餐3 | 38 | 300 | 50 | ||
| 套餐4 | 48 | 500 | 50 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
19.一天,昆明的最高气温为6℃,最低气温为-4℃,那么这天的最高气温比最低气温高( )
| A. | 10℃ | B. | -10℃ | C. | 2℃ | D. | -2℃ |
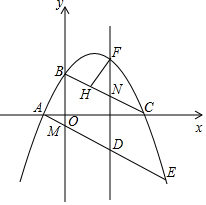 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m) 已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.
已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.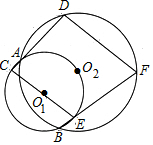 如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.
如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.