题目内容
20.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
分析 先根据二次函数的性质得到抛物线的对称轴为直线x=-1,然后比较三个点离直线x=-1的远近得到y1、y2、y3的大小关系.
解答 解:∵二次函数的解析式为y=-(x+1)2+m,
∴抛物线的对称轴为直线x=-1,
∵A(-2,y1)、B(1,y2)、C(2,y3),
∴点C离直线x=-1最远,点A离直线x=-1最近,
抛物线开口向下,
∴y1>y2>y3.
故选:A.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
5. 已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
 已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
已知,a,b两数在数轴上的位置如图,下列各式成立的是( )| A. | ab>0 | B. | (a+1)(b+1)>0 | C. | a+b>0 | D. | (a-1)(b-1)>0 |
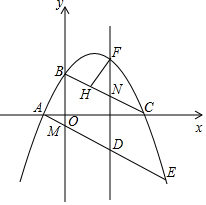 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)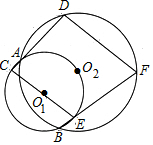 如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.
如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.