题目内容
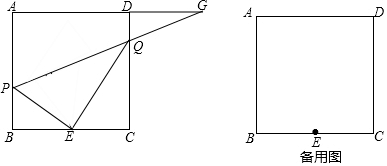
9.已知:正方形ABCD的边长为4,点E为BC边的中点,点P为AB边上一动点,联结PE,过E作EQ⊥PE交边CD于Q,直线PQ交直线AD于点G.(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,设BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围.
分析 (1)由于EQ⊥PE,所以易证△PEB∽△EQC,所以$\frac{PB}{EC}=\frac{BE}{CQ}$,进而求出CQ长度.
(2)过点P作PF⊥CD于点F,易证△QDG∽△QPF,利用相似三角形的性质即可求出y与x的关系式.
解答 解:(1)∵点E为BC边的中点,
∴BE=CE=2,
∵EQ⊥PE,
∴∠PEQ=90°,
∴∠PEB+∠QEC=∠EQC+∠QEC=90°,
∴∠PEB=∠EQC,
∵∠B=∠C=90°,
∴△PEB∽△EQC,
∴$\frac{PB}{EC}=\frac{BE}{CQ}$
∴CQ=$\frac{8}{3}$,
(2)由(1)可知:△PEB∽△EQC,
∴$\frac{PB}{EC}=\frac{BE}{CQ}$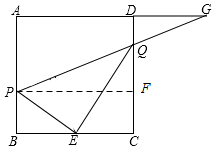
∴CQ=$\frac{4}{x}$,
当CQ=4时,
此时x=1,
∴1≤x≤4,
过点P作PF⊥CD于点F,
∴△QPF∽△QGD,
∴$\frac{PF}{DG}=\frac{QF}{DQ}$
∵CF=PB=x,
∴QF=CQ-CF=$\frac{4}{x}-x$,
DQ=CD-CQ=4-$\frac{4}{x}$
∴$\frac{4}{y}=\frac{\frac{4}{x}-x}{4-\frac{4}{x}}$,
化简可得:y=$\frac{4(4x-4)}{4-{x}^{2}}$(1≤x≤4)
点评 本题考查相似三角形的应用,解题的关键是证明△PEB∽△EQC,利用相似三角形的性质求出CQ的长度,本题属于中等题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )| A. | 26° | B. | 52° | C. | 60° | D. | 64° |
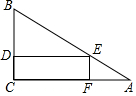 一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上.
一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为4.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为4.