题目内容
14. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为4.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为4.
分析 首先证明BD=AD,然后再根据在直角三角形中,斜边上的中线等于斜边的一半可得CP=$\frac{1}{2}$BD.
解答 解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠A=∠DBA,
∴AD=BD=8,
∵P点是BD的中点,∠ACB=90°,
∴CP=$\frac{1}{2}$BD=4,
故答案为:4.
点评 此题主要考查了直角三角形的性质,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.直角三角形的两条直角边长分别是3,4,则该直角三角形的斜边长是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.将正整数依次按如表规律排成四列,请根据表中的排列规律回答下列问题:
(1)第6行第2列的数是多少?
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
 如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k=$\frac{4}{3}$.
如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k=$\frac{4}{3}$. 如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.
如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.
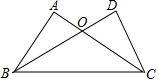 如图,AC、BD相交于点O,AB=CD,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是∠A=∠D.
如图,AC、BD相交于点O,AB=CD,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是∠A=∠D.