题目内容
17.例:解分式不等式$\frac{2x}{x+1}$>1解:当x+1>0时,去分母得2x>x+1;当x+1<0时,去分母得2x<x+1
∴$\left\{\begin{array}{l}{x+1>0}\\{2x>x+1}\end{array}\right.$或$\left\{\begin{array}{l}{x+1<0}\\{2x<x+1}\end{array}\right.$,
分别解不等式组得:x>1或x<-1
所以原不等式的解集为:x>1或x<-1
根据以上材料,解决下面问题:
(1)请你写出一个分式不等式;
(2)解分式不等式$\frac{3x+2}{x-3}$≥1;
(3)解分式不等式$\frac{-2{x}^{2}+3x}{{x}^{2}+2x+1}$<-2.
分析 (1)根据题意写出一个分母中有未知数的不等式即可;
(2)类比以上作法分x-3>0、x-3<0两种情况,分别去分母得到两个不等式组,解不等式组可得;
(3)观察到不等式分母x2+2x+1=(x+1)2≥0,直接去分母可得不等式,解不等式可得解集.
解答 解:(1)$\frac{2x}{x-2}<1$;
(2)当x-3>0时,去分母,得:3x+2≥x-3;
当x-3<0时,去分母,得:3x+2≤x-3;
∴$\left\{\begin{array}{l}{x-3>0}\\{3x+2≥x-3}\end{array}\right.$或$\left\{\begin{array}{l}{x-3<0}\\{3x+2≤x-3}\end{array}\right.$,
分别解不等式组,得:x>3或x≤-5,
所以原不等式的解集为:x>3或x≤-5;
(3)∵x2+2x+1=(x+1)2≥0,
∴去分母,得:-2x2+3x<-2(x2+2x+1),
解得:x<-$\frac{2}{7}$,
又(x+1)2≠0,即x≠-1,
∴原不等式的解集为:x<-$\frac{2}{7}$且x≠-1.
点评 本题主要考查解分式不等式的能力和类比的作法,熟知不等式的基本性质是解题的根本,理解和掌握例题的作法是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
11.方程组$\left\{\begin{array}{l}{x+3y=5}\\{2x-3y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ |
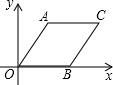 ?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).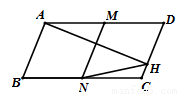
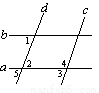
 ∥
∥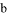 B. ∵∠1=∠2,∴
B. ∵∠1=∠2,∴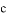 ∥
∥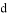 D. ∵∠1=∠3,∴
D. ∵∠1=∠3,∴