题目内容
11.方程组$\left\{\begin{array}{l}{x+3y=5}\\{2x-3y=1}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ |
分析 用加减消元法解方程组,即可解答.
解答 解:$\left\{\begin{array}{l}{x+3y=5①}\\{2x-3y=1②}\end{array}\right.$
①+②得:3x=6,
解得:x=2,
把x=2代入①得:2+3y=5,
解得:y=1,
∴方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$
故选:B.
点评 本题考查了解二元一次方程组,解决本题的关键是用加减消元法解方程组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

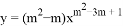 是反比例函数,则( )
是反比例函数,则( )