题目内容

6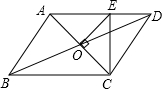．如图所示，平行四边形ABCD的周长为4a，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长是（　　）
A．aB．2aC．3aD．4a

分析 由?ABCD的周长为4a，可得AD+CD=2a，OA=OC，又由OE⊥AC，根据线段垂直平分线的性质，可证得AE=CE，继而求得△DCE的周长=AD+CD．

解答 解：∵?ABCD的周长为4a，
∴AD+CD=2a，OA=OC，
∵OE⊥AC，
∴AE=CE，
∴△DCE的周长为：CD+DE+CE=CD+DE+AE=CD+AD=2a．
故选：B．

点评 此题考查了平行四边形的性质以及线段垂直平分线的性质．注意得到△DCE的周长=AD+CD是关键．

练习册系列答案
相关题目
10．如果a（a-b）2-（b-a）=（a-b）G，那么G是（　　）
A．a（a-b）B．-a（a-b）C．a2-ab-1D．a2-ab+1
17．如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分，已知抛物线的对称轴是x=2，与x轴的一个交点是（-1，0），有下列结论：
①abc＞0；
②4a-2b+c＜0；
③4a+b=0；
④抛物线与x轴的另一个交点是（5，0）；
⑤点（-3，y1），（6，y2）都在抛物线上，则有y1=y2．
其中正确的是（　　）
A．4个B．3个C．2个D．1个
14．已知分式$\frac{2x+1}{x+2}$，当x=-2时，分式没有意义；当x=-$\frac{1}{2}$时，分式的值为0；当x=2时，分式的值为$\frac{5}{4}$．
1．已知五边形ABCDE∽五边形FGHIJ，相似比为1：2，若五边形ABCDE的周长和面积分别为6和15，则五边形FGHIJ的周长和面积分别为（　　）
A．12和30B．12和60C．24和30D．24和60
11．如图，一张正方形纸板的边长为2cm，将它剪去4个全等的直角三角形（图中阴影部分）．设AE=BF=CG=DH=xcm，四边形EFGH的面积为ycm2，
（1）求y关于x的函数表达式和自变量x的取值范围；
（2）求四边形EFGH的面积为3cm2时的x值；
（3）四边形EFGH的面积可以为1.5cm2吗？请说明理由．
18．在Rt△ABC中，已知∠C=90°，∠A=40°，BC=3，则AC等于（　　）
A．3tan50°B．3sin50°C．3tan40°D．3sin40°
15．“戒烟一小时，健康亿人行”，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：
A．顾客出面制止；
B．劝说进吸烟室；
C．餐厅老板出面制止；
D．无所谓．
他将调查结果绘制了两幅不完整的统计图，请你根据图中的信息回答下列问题：

（1）这次抽样的样本容量是多少？
（2）请将统计图①补充完整．
（3）在统计图②中，求“无所谓”部分所对应的圆心角的度数．
16．在数轴上，位于-3和3之间的点有（　　）
A．7个B．5个C．4个D．无数个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网