题目内容
11. 如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=xcm,四边形EFGH的面积为ycm2,
如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=xcm,四边形EFGH的面积为ycm2,(1)求y关于x的函数表达式和自变量x的取值范围;
(2)求四边形EFGH的面积为3cm2时的x值;
(3)四边形EFGH的面积可以为1.5cm2吗?请说明理由.
分析 (1)先证出四边形EFGH为正方形,用未知数x表示其任一边长,根据正方形面积公式即可解决问题;
(2)代入y值,解一元二次方程即可;
(3)将面积y=2x2-4x+4改写成完全平方的形式,可得知y≥2,故不能为cm2.
解答 解:(1)∵在正方形纸上剪去4个全等的直角三角形,
∴∠AHE=∠DGH,∠DGH+∠DHG=90°,HG=HE,
∵∠EHG=180°-∠AHE-∠DHG,
∴∠EHG=90°,四边形EFGH为正方形,
在△AEH中,AE=x,AH=BE=AB-AE=2-x,∠A=90°,
∴HE2=AE2+AH2=x2+(2-x)2=2x2-4x+4,
正方形EFGH的面积y=HE2=2x2-4x+4,
∵AE,AH均为正值,
∴0<x<2,
故y关于x的函数表达式为:y=2x2-4x+4,自变量x的取值范围0<x<2.
(2)将y=3代入y=2x2-4x+4中,整理得:2x2-4x+1=0,
解得:x1=1+$\frac{\sqrt{2}}{2}$,x2=1-$\frac{\sqrt{2}}{2}$,
故四边形EFGH的面积为3cm2时的x的值为1+$\frac{\sqrt{2}}{2}$或1-$\frac{\sqrt{2}}{2}$.
(3)四边形EFGH的面积为:y=2x2-4x+4=2(x-1)2+2,(0<x<2),
∵(x-1)2≥0,
∴y≥2,
四边形EFGH的面积不能为1.5cm2.
点评 本题考查二次函数的应用,解题的关键是找准数量关系,对于第三问,只要将关系式转化成完全平方的形式,即可看出结论.

练习册系列答案
相关题目
19.如果零上5℃记作+5℃,那么零下5℃记作( )
| A. | -5 | B. | -5℃ | C. | -10 | D. | -10℃ |
6.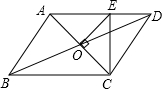 如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )
如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )
 如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )
如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )| A. | a | B. | 2a | C. | 3a | D. | 4a |
16.某电视台组织知识竞赛,共设20道选择题,每题必答,如表记录了3个参赛者的得分情况.
(1)参赛者小婷得76分,她答对了几道题?
(2)参赛者小明说他得了80分.你认为可能吗?为什么?
(1)参赛者小婷得76分,她答对了几道题?
(2)参赛者小明说他得了80分.你认为可能吗?为什么?
| 参赛者 | 答对题数 | 答错题数 | 总得分 |
| 甲 | 20 | 0 | 100 |
| 乙 | 19 | 1 | 94 |
| 丙 | 14 | 6 | 64 |
20.某县2013年对教育的投入为2500万元,2015年对教育的投入为3500万元,求该县2013-2015年对教育投入的年平均增长率,假设该县投入教育经费的年平均增长率为x,则依题意所列方程正确的是( )
| A. | 2500x2=3500 | B. | 2500(1+x)2=3500 | ||
| C. | 2500(1+x%)2=3500 | D. | 2500(1+x)+2500(1+x)2=3500 |