题目内容
2．计算：（1）$\frac{{a}^{2}-6a+9}{4-{b}^{2}}÷\frac{3-a}{2+b}•\frac{{a}^{2}}{3a-9}$
（2）（$\frac{x-2}{x+2}+\frac{4x}{{x}^{2}-4}$）$÷\frac{1}{{x}^{2}-4}$，其中x=-3．
分析 （1）首先把分子和分母分解因式，把除法转化为乘法，然后进行约分即可求解；
（2）首先把括号内的分式通分相加，把除法转化为乘法，然后进行乘法运算即可化简，再代入数值计算即可．
解答 解：（1）原式=$\frac{（a-3）^{2}}{（2+b）（2-b）}$•$\frac{2+b}{3-a}$•$\frac{{a}^{2}}{3（a-3）}$
=$\frac{{a}^{2}}{3（2-b）}$；
（2）原式=$\frac{（x-2）^{2}+4x}{{x}^{2}-4}$•（x2-4）
=（x-2）2+4x
=x2-4x+4+4x
=x2+4．
当x=-3时，原式=9+4=13．
点评 本题考查了分式的混合运算，分式混合运算要注意先去括号；分子、分母能因式分解的先因式分解；除法要统一为乘法运算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一个圆柱体钢块，从正中间挖去一个长方体得到的零件毛坯的俯视图如图，其主视图是（ ）
13．给出下列命题：
①垂直于弦的直线平分弦；
②平分弦的直径必垂直于弦，并且平分弦所对的两条弧；
③相等的弦所对的圆心角相等；
④等弧所对的圆心角相等；
其中正确的命题有（ ）
①垂直于弦的直线平分弦；
②平分弦的直径必垂直于弦，并且平分弦所对的两条弧；
③相等的弦所对的圆心角相等；
④等弧所对的圆心角相等；
其中正确的命题有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
10．九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如表：
已知该运动服的进价为每件60元，设售价为x元．
（1）求月销售m件与售价x元/件之间的函数表达式．
（2）设销售该运动服的月利润为y元，写出y与x之间的函数表达式，并求出售价x为多少时，当月的利润最大，最大利润是多少？
| 售价x（元/件） | 100 | 110 | 120 | 130 | … |
| 月销量m（件） | 200 | 180 | 160 | 140 | … |
（1）求月销售m件与售价x元/件之间的函数表达式．
（2）设销售该运动服的月利润为y元，写出y与x之间的函数表达式，并求出售价x为多少时，当月的利润最大，最大利润是多少？
如图，在Rt△OAB中，OA=2，AB=1，OA在数轴上，点O与原点重合，以原点为圆心，线段OB长为半径画弧，交数轴正半轴于一点，则这个点表示的实数是$\sqrt{5}$．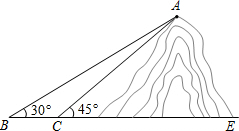
如图，小明想测山高和索道的长度，他在B处仰望山顶A，测得仰角∠B=30°．再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=45°．