题目内容
14.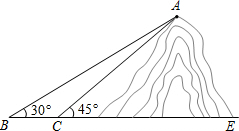 如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.
如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(带根号即可).
分析 (1)作AH⊥BE于H,设AC=xm,根据正切的概念表示出CH、BH,根据题意列出方程,解方程即可;
(2)根据等腰直角三角形的性质解答即可.
解答 解:(1)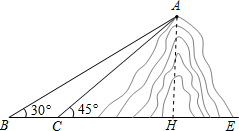 作AH⊥BE于H,
作AH⊥BE于H,
设AC=xm,
∵∠ACE=45°,
∴CH=AH=xm,
tanB=$\frac{AH}{BH}$,
∴BH=$\sqrt{3}$x,
则BH-CH=BC,即$\sqrt{3}$x-x=80,
解得x=40($\sqrt{3}$+1).
答:这座山的高度为40($\sqrt{3}$+1)m;
(2)∵∠ACE=45°,
∴AC=$\sqrt{2}$AH=40($\sqrt{6}$+$\sqrt{2}$)m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确作出辅助线、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列命题中,是真命题的是( )
| A. | 角是轴对称图形,角平分线是它的对称轴 | |
| B. | 线段是轴对称图形,并且只有一条对称轴 | |
| C. | 三角形的一个外角等于它任意两个内角的和 | |
| D. | 在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半 |
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;
 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车距A地的距离y(km)与甲车行驶时间x(h)的函数图象.
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车距A地的距离y(km)与甲车行驶时间x(h)的函数图象.