题目内容
20．
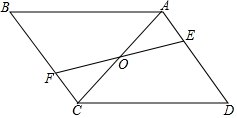已知：如图，平行四边形 ABCD中，点E、F分别在AD、BC上，且ED=BF，EF与AC相交于点O．求证：OA=OC．
分析 根据平行四边形的性质和ASA易证△AOE≌△COF，根据全等三角形的性质可得OA=OC．
解答 证明：在平行四边形ABCD中，
∵AD∥BC，
∴∠EAO=∠FCO，∠AEO=∠CFO，AD=BC，
又∵ED=BF，
∴AE=CF，
在△AOE与△COF中，
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AE=CF}\\{∠AEO=∠CFO}\end{array}\right.$，
∴△AOE≌△COF（ASA），
∴OA=OC．
点评 本题考查了平行四边形的性质及全等三角形的判定，解答本题需要掌握两点，①平行四边形的对边相等且平行，②全等三角形的对应边、对应角分别相等．
练习册系列答案
名校通行证有效作业系列答案
相关题目
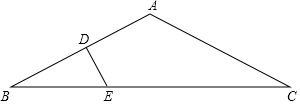如图，△ABC中，AB=AC=2$\sqrt{5}$，BC=8，AB的垂直平分线交AB于点D，交BC于点E，设△BDE的面积为S1，四边形ADEC的面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$．
8．若A（1，y1）、B（2，y2）、C（-3，y3）为双曲线$y=\frac{k-1}{x}$上三点，且y1＞y2＞0＞y3，则k的范围为（ ）
| A． | k＞0 | B． | k＞1 | C． | k＜1 | D． | k≥1 |
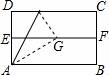如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为60°．
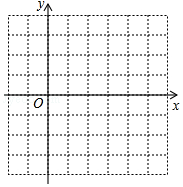请在网格坐标系中画出二次函数y=x2-4x+1的大致图象（注：图中小正方形网格的边长为1），根据图象填空：