题目内容
8.若A(1,y1)、B(2,y2)、C(-3,y3)为双曲线$y=\frac{k-1}{x}$上三点,且y1>y2>0>y3,则k的范围为( )| A. | k>0 | B. | k>1 | C. | k<1 | D. | k≥1 |
分析 根据A(1,y1)、B(2,y2)为双曲线$y=\frac{k-1}{x}$上两点,且y1>y2>0可得y随x的增大而减小,进而可得k-1>0,再解即可.
解答 解:∵A(1,y1)、B(2,y2)为双曲线$y=\frac{k-1}{x}$上两点,且y1>y2>0,
∴y随x的增大而减小,
∴k-1>0,
∴k>1,
故选:B.
点评 此题主要考查了反比例函数的性质,反比例函数y=$\frac{k}{x}$的性质,当k>0时,图象的两支在第一三象限,在图象的每一支上,y随x的增大而减小

练习册系列答案
相关题目
18.2012年,我市参加中考的学生约为33200万人,用科学记数法表示为( )
| A. | 0.332×105人 | B. | 33.2×106人 | C. | 3.32×108人 | D. | 332×108 人 |
19.在如图所示的3×3方阵图中,处于同一横行、同一竖列、同一斜对角线上的3个数之和都相等.现在方阵图
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
| -2 | -4 | 3x+6 |
| 4 | x | |
| -x-6 |
3.在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.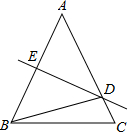 在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
 在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )
在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是( )| A. | 50° | B. | 40° | C. | 65° | D. | 15° |
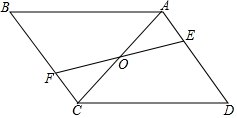 已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O.
已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O.