题目内容
7．若关于x的方程3x2-kx+k=0有两个相等的实数根，则常数k的值为0或12．分析 由方程有两个相等的实数根结合根的判别式可得出关于k的一元二次方程，解方程即可得出结论．
解答 解：∵关于x的方程3x2-kx+k=0有两个相等的实数根，
∴△=0，即（-k）2-4×3k=k2-12k=0，
解得：k1=0，k2=12．
故答案为：0或12．
点评 本题考查了根的判别式以及一元二次方程的解，解题的关键是根据根的个数得出关于k的一元二次方程．本题属于基础题，难度不大，解决该题型题目时，根据根的个数结合根的判别式得出不等式（或方程）是关键．
练习册系列答案
相关题目
如图点A、B、C在⊙O上，CO延长线交AB于点D，∠A=60°，∠B=30°，则∠ADC的度数为90°．
18．
如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，∠AED=115°，则∠B的度数是（ ）
如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，∠AED=115°，则∠B的度数是（ ）| A． | 50° | B． | 75° | C． | 80° | D． | 100° |
如图，在平面直角坐标系中，Rt△OAB的顶点B在x轴的正半轴上，已知∠OBA=90°，OB=3，sin∠AOB=$\frac{4}{5}$．反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点A．
某厂家生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD，线段CD分别表示该产品每千克生产成本y1（单位：元），销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
12．在实数$\sqrt{7}$，6，-$\frac{1}{3}$，2.5中，无理数是（ ）
| A． | $\sqrt{7}$ | B． | 6 | C． | -$\frac{1}{3}$ | D． | 2.5 |
19．
如图，已知直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（ ）
如图，已知直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（ ）| A． | 35° | B． | 40° | C． | 55° | D． | 75° |
16．计算6×（-2）-12÷（-4）的结果是（ ）
| A． | 10 | B． | 0 | C． | -3 | D． | -9 |
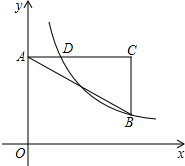如图在直角坐标系中，点A在y轴正半轴上，AC∥x轴，点B，C的横坐标都是3，且BC=2，点D在AC上且横坐标为1，若反比例函数y=$\frac{k}{x}$（x＞0）图象象经过点B，D，求k的值．