题目内容
16.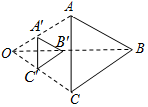 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:8 | D. | 1:9 |
分析 根据位似变换的性质得到A′B′∥AB,A′C′∥AC,根据平行线的性质求出△A'B'C'与△ABC的相似比,根据相似三角形的性质得到面积比.
解答 解:由位似变换的性质可知,A′B′∥AB,A′C′∥AC,
∴$\frac{OA′}{OA}$=$\frac{OB′}{OB}$=$\frac{1}{3}$,
∴$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$=$\frac{1}{3}$,
∴△A'B'C'与△ABC的相似比为1:3,
∴△A'B'C'与△ABC的面积的比1:9,
故选:D.
点评 本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
6. 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )| A. | 2 | B. | 8 | C. | $4\sqrt{3}$ | D. | $4\sqrt{5}$ |
1.一个物体做左右方向的运动,规定向右运动6m记作+6m,那么向左运动8m记作( )
| A. | +8m | B. | -8m | C. | +14m | D. | -14m |
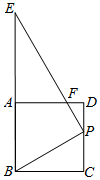 如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.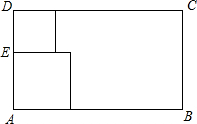 如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?
如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?