题目内容
17.化简:$\frac{{{x^2}+7x+12}}{{{x^2}-8x+15}}$÷$\frac{{{x^2}+3x-4}}{{{x^2}-5x+6}}$÷$\frac{{{x^2}+x-6}}{{{x^2}-4x-5}}$.分析 先将分子分母因式分解,然后利用分式的基本性质化简即可.
解答 解:原式=$\frac{(x+3)(x+4)}{(x-3)(x-5)}$•$\frac{(x-2)(x-3)}{(x+4)(x-1)}$•$\frac{(x-5)(x+1)}{(x+3)(x-2)}$
=$\frac{x+1}{x-1}$
点评 本题考查分式的乘除运算,涉及十字相乘法,解题的关键是先将分子分母因式分解,然后约分即可求出答案.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12. 如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是( )
如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是( )
 如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是( )
如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是( )| A. | P是m上到A、B距离之和最短的点,Q是m上到A、B距离相等的点 | |
| B. | Q是m上到A、B距离之和最短的点,P是m上到A、B距离相等的点 | |
| C. | P、Q都是m上到A、B距离之和最短的点 | |
| D. | P、Q都是m上到A、B距离相等的点 |
2.下列说法中,正确的是( )
| A. | 不可能事件发生的概率是0 | |
| B. | 打开电视机正在播放动画片,是必然事件 | |
| C. | 随机事件发生的概率是 $\frac{1}{2}$ | |
| D. | 对“梦想的声音”节目收视率的调查,宜采用普查 |
 如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )
如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )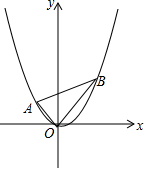 如图,二次函数y=$\frac{2}{3}$x2-$\frac{1}{3}$x,图象过△ABC三个顶点,其中A(-1,m),B(n,n)
如图,二次函数y=$\frac{2}{3}$x2-$\frac{1}{3}$x,图象过△ABC三个顶点,其中A(-1,m),B(n,n) 如图,在圆内接四边形ABCD中,∠A=52.5°,∠B=97.5°,∠AOB=120°(O为圆心),AB=a,BC=b,CD=c,DA=d,用a、b、c、d表示四边形ABCD的面积.
如图,在圆内接四边形ABCD中,∠A=52.5°,∠B=97.5°,∠AOB=120°(O为圆心),AB=a,BC=b,CD=c,DA=d,用a、b、c、d表示四边形ABCD的面积.