Question

6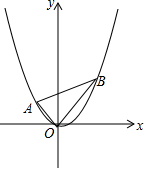．如图，二次函数y=$\frac{2}{3}$x²-$\frac{1}{3}$x，图象过△ABC三个顶点，其中A（-1，m），B（n，n）
求：①求A，B坐标；
②求△AOB的面积．

Answer 1

分析 （1）先根据二次函数图象上点的坐标特征，把A（-1，m），B（n，n）分别代入抛物线解析式可求出m和n的值，则得到A（-1，1），B（2，2）；
（2）利用待定系数法求出直线AB的解析式，则可确定C点坐标，于是可根据三角形面积公式计算△AOB的面积

解答 解：（1）把A（-1，m）代入y=$\frac{2}{3}$x²-$\frac{1}{3}$x得m=$\frac{2}{3}$+$\frac{1}{3}$=1，则A（-1，1），
把B（n，n）代入y=$\frac{2}{3}$x²-$\frac{1}{3}$x得$\frac{2}{3}$n²-$\frac{1}{3}$n=n，解得n₁=0（舍去），n₂=2，则B（2，2）；
（2）设直线AB的解析式为y=kx+b，
把A（-1，1），B（2，2）分别代入得$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$，
所以直线AB的解析式为y=$\frac{1}{3}$x+$\frac{4}{3}$，
当x=0时，y=$\frac{1}{3}$x+$\frac{4}{3}$=$\frac{4}{3}$，则C点坐标为（0，$\frac{4}{3}$），
所以△AOB的面积=△AOC的面积+△BOC的面积=$\frac{1}{2}$×$\frac{4}{3}$×（1+2）=2．

点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了三角形面积公式和待定系数法一次函数解析式．