题目内容
12．
如图，直线m同侧有A、B两点，A、A′关于直线m对称，A、B关于直线n对称，直线m与A′B和n分别交于P、Q，下面的说法正确的是（ ）| A． | P是m上到A、B距离之和最短的点，Q是m上到A、B距离相等的点 | |
| B． | Q是m上到A、B距离之和最短的点，P是m上到A、B距离相等的点 | |
| C． | P、Q都是m上到A、B距离之和最短的点 | |
| D． | P、Q都是m上到A、B距离相等的点 |
分析 只要证明点P是m上到A、B距离之和最短的点，同理可得Q是n上到A、B距离相等的点．
解答 解：如图，
在直线m上取一点P′，
∵A、A′关于直线m对称，
∴PA=PA′．P′A=P′A′，
∵P′A+P′B=P′A′+P′B≥A′B，即P′A+P′B≥PA+PB，
∴点P是m上到A、B距离之和最短的点，同理：Q是n上到A、B距离相等的点，
故选A．
点评 本题考查轴对称-最短问题、两点之间线段最短等知识，解题的关键是灵活运用对称解决最短问题，属于中考常考题型．
练习册系列答案
相关题目
作图：已知∠AOB，试在∠AOB内确定一点P，使P到OA、OB的距离相等，并且到M、N两点的距离也相等．
7．樱桃是阿西罗拉樱桃的中文名称，原产于热带美洲西印度群岛加勒比海地区，以富含维生素C而闻名于世，某种植樱桃的农户共摘收了1050千克的樱桃，为寻求合适的销售价格，进行了5天试销，试销情况如下：
（1）若y与x满足反比例函数的关系，求y关于x的函数表达式；
（2）在试销5天后，该农户决定将这批樱桃的售价定为12元/千克，求剩余的樱桃预计还要多少天才可以全部售完？
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
| 售价x（元/千克） | 18 | 15 | 12 | 10 | 9 |
| 销售量y（千克） | 50 | 60 | 75 | 90 | 100 |
（2）在试销5天后，该农户决定将这批樱桃的售价定为12元/千克，求剩余的樱桃预计还要多少天才可以全部售完？
4．
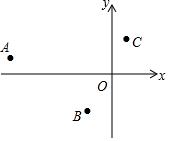在平面直角坐标系xOy中，二次函数y=ax2+bx的图象经过点A，B，C，则对系数a和b判断正确的是（ ）
在平面直角坐标系xOy中，二次函数y=ax2+bx的图象经过点A，B，C，则对系数a和b判断正确的是（ ）| A． | a＞0，b＞0 | B． | a＜0，b＜0 | C． | a＞0，b＜0 | D． | a＜0，b＞0 |