��Ŀ����
������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ��(�����㹻��)����28m�������Χ��һ�����λ�ABCD(���ֻΧAB��BC����)����AB��xm.
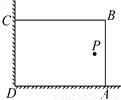
(1)���������Ϊ192m2����x��ֵ��
(2)����P����һ������ǽCD��AD�ľ���ֱ���13m��6m��Ҫ�������Χ�ڻ���(���߽磬���������Ĵ�ϸ)�������S�����ֵ��
 (1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1...
(1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1...
��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�E����CBD��90�㣬BC��4��BE��ED��3��AC��10�����ı���ABCD�����Ϊ( )
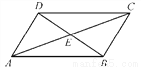
A. 6 B. 12 C. 20 D. 24
 D
�������������������Rt��CBE�У��ɹ��ɶ��������EC=5������AC=10������AE=EC=5.���ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο��ж��ı���ABCD��ƽ���ı��Σ�����ƽ���ı���ABCD�����ΪBC��BD=4��6=24���ʴ�ѡD.
D
�������������������Rt��CBE�У��ɹ��ɶ��������EC=5������AC=10������AE=EC=5.���ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο��ж��ı���ABCD��ƽ���ı��Σ�����ƽ���ı���ABCD�����ΪBC��BD=4��6=24���ʴ�ѡD. ��ͼ��������ABCD�У�AB��8cm���Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ��B��C����ͬʱ��������1cm/s���ٶ���BC��CD�˶�������C��Dʱֹͣ�˶������˶�ʱ��Ϊt(s)����OEF�����ΪS(cm2)����S(cm2)��t(s)�ĺ�����ϵ����ͼ���ʾΪ( )
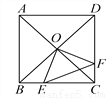
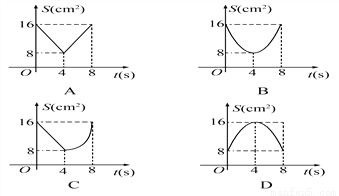
A. A B. B C. C D. D
 B
������������������ɵ�E��F�ֱ��B��C����ͬʱ��������1cm/s���ٶ���BC��CD�˶����õ�BE=CF=t����CE=8��t���ٸ��������ε����ʵ�OB=OC����OBC=��OCD=45�㣬Ȼ����ݡ�SAS�����жϡ�OBE�ա�OCF������S��OBE=S��OCF������S�ı���OECF=S��OBC=16������S=S�ı���OECF��S��CEF=16����8��t��t��Ȼ���䷽�õ�S=��t��4��2+8��...
B
������������������ɵ�E��F�ֱ��B��C����ͬʱ��������1cm/s���ٶ���BC��CD�˶����õ�BE=CF=t����CE=8��t���ٸ��������ε����ʵ�OB=OC����OBC=��OCD=45�㣬Ȼ����ݡ�SAS�����жϡ�OBE�ա�OCF������S��OBE=S��OCF������S�ı���OECF=S��OBC=16������S=S�ı���OECF��S��CEF=16����8��t��t��Ȼ���䷽�õ�S=��t��4��2+8��... �����¼�Ϊ��Ȼ�¼����ǣ�������
A. С���μӱ�����ѧ���ԣ��ɼ���150��
B. ij����˶�Ա���һ�Σ����а���
C. ���ӻ���CCTV��һ��Ŀ���ڲ�������
D. �ڴ���װ��2�������1������������2�������б��к���
 D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD��
D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD�� �����¼��У���������¼����ǣ�������
A. ͨ��ˮ���ȵ�100��ʱ����
B. ����Т��ij���������£����Ϊ��150��
C. һ������װ��5������������һ���Ǻ���
D. �����Ա�ڷ�������Ͷ��һ�Σ�δͶ��
 D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD.
D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD. ��ͼ���߶�AB�ij�Ϊ2��CΪAB��һ�����㣬�ֱ���AC��BCΪб����AB��ͬ������������ֱ�������Ρ�ACD�͡�BCE����ôDE������Сֵ��______________��

 4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ...
4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ... ��ͼ���ӵ�����ֱ�����׳�һ��С��С��ĸ߶�h����λ��m����С���˶�ʱ��t����λ��s��֮��Ĺ�ϵʽΪh=30t-5t2����ôС����׳������䵽��������Ҫ��ʱ���ǣ�������
A. 6s B. 4s C. 3s D. 2s
 A
�������������������С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2����h=0����õ���ֵ֮�������Ҫ��õĽ����
��С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2�� ��h=0����5t2+30t=0 ��ã�t1=0��t2=6
��t=6��С����׳������䵽��������Ҫ��ʱ����6�룮
A
�������������������С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2����h=0����õ���ֵ֮�������Ҫ��õĽ����
��С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2�� ��h=0����5t2+30t=0 ��ã�t1=0��t2=6
��t=6��С����׳������䵽��������Ҫ��ʱ����6�룮 ����A(3��2)��x������ƽ��4����λ���ȵõ���A�䣬���A�����ԭ��ԳƵĵ��������( )
A. (-3��2) B. (-1��2) C. (1��2) D. (1��-2)
 D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD��
D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD�� ��֪һֱ�DZߺ�����ֱ�DZߵĶԽǣ�����ֱ��������(�ó߹���ͼ����д��������Ҫ������ͼ�ۼ�)��
 ������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������...
������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������... 
