题目内容
初一(3)班共有学生50人,其中男生有21人,女生29人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性__(填“大”或“小”).
 小
【解析】只要比较男生人数与女生人数的多少即可.
【解析】
男生人数少于女生人数,因而找到男生的可能性比找到女生的可能性小.
小
【解析】只要比较男生人数与女生人数的多少即可.
【解析】
男生人数少于女生人数,因而找到男生的可能性比找到女生的可能性小.
我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
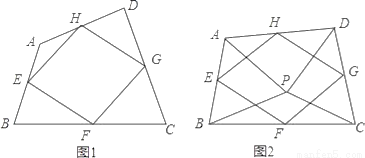
 (1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.
【解析】试题分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠B...
(1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.
【解析】试题分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠B... 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )
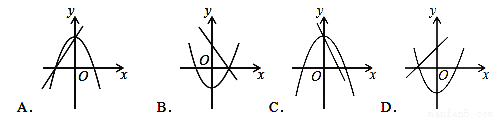
A. A B. B C. C D. D
 C
【解析】解:A.由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,故A错误;
B.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故B错误;
C.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故C正确;...
C
【解析】解:A.由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,故A错误;
B.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故B错误;
C.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故C正确;... 如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
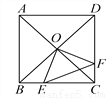
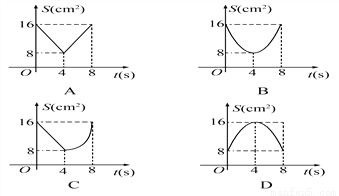
A. A B. B C. C D. D
 B
【解析】试题分析:由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣(8﹣t)t,然后配方得到S=(t﹣4)2+8(...
B
【解析】试题分析:由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣(8﹣t)t,然后配方得到S=(t﹣4)2+8(... 从1,2,3,4,5这五个数中任意取两个相乘,问:
(1)积为偶数,属于哪类事件?有几种可能情况?
(2)积为奇数,属于哪类事件?有几种可能情况?
(3)积为无理数,属于哪类事件?
 (1)可能事件,7;(2)可能事件,3;(3)不可能事件
【解析】试题分析:(1),(2)由于五个数中任意取两数相乘有奇数有偶数,所以(1)(2)都为不确定事件,分别写出乘积为偶数与为奇数的情况,即可看出分别有几种情况.
(3)由于五个数都是有理数,他们的乘积也一定为有理数,不可能为无理数,所以(3)为不可能事件.
试题解析: 取任意两个数相乘,可能的结果如下表所示(重复的不留在表中...
(1)可能事件,7;(2)可能事件,3;(3)不可能事件
【解析】试题分析:(1),(2)由于五个数中任意取两数相乘有奇数有偶数,所以(1)(2)都为不确定事件,分别写出乘积为偶数与为奇数的情况,即可看出分别有几种情况.
(3)由于五个数都是有理数,他们的乘积也一定为有理数,不可能为无理数,所以(3)为不可能事件.
试题解析: 取任意两个数相乘,可能的结果如下表所示(重复的不留在表中... 下列事件为必然事件的是( )
A. 小王参加本次数学考试,成绩是150分
B. 某射击运动员射靶一次,正中靶心
C. 打开电视机,CCTV第一套节目正在播放新闻
D. 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
 D
【解析】试题分析:A.小王参加本次数学考试,成绩是150分是随机事件,故A选项错误;
B.某射击运动员射靶一次,正中靶心是随机事件,故B选项错误;
C.打开电视机,中央一套节目正在播放新闻是随机事件,故C选项错误.
D.口袋中装有两个红球和一个白球,从中摸出两个球,其中必有红球是必然事件,故D选项正确;
故选D.
D
【解析】试题分析:A.小王参加本次数学考试,成绩是150分是随机事件,故A选项错误;
B.某射击运动员射靶一次,正中靶心是随机事件,故B选项错误;
C.打开电视机,中央一套节目正在播放新闻是随机事件,故C选项错误.
D.口袋中装有两个红球和一个白球,从中摸出两个球,其中必有红球是必然事件,故D选项正确;
故选D. 下列事件中,属于随机事件的是( )
A. 通常水加热到100℃时沸腾
B. 测量孝感某天的最低气温,结果为﹣150℃
C. 一个袋中装有5个黑球,从中摸出一个是黑球
D. 篮球队员在罚球线上投篮一次,未投中
 D
【解析】试题解析:结合所学的随机事件与必然事件的意义,A必然发生,是必然事件;B一定不会发生,是必然事件;C一定会发生,是必然事件;D 罚球投篮一次未投中是可能发生的,属于随机事件.故选D.
D
【解析】试题解析:结合所学的随机事件与必然事件的意义,A必然发生,是必然事件;B一定不会发生,是必然事件;C一定会发生,是必然事件;D 罚球投篮一次未投中是可能发生的,属于随机事件.故选D. 如图,从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A. 6s B. 4s C. 3s D. 2s
 A
【解析】试题分析:由小球高度h与运动时间t的关系式h=30t﹣5t2,令h=0,解得的两值之差便是所要求得的结果.
由小球高度h与运动时间t的关系式h=30t﹣5t2. 令h=0,﹣5t2+30t=0 解得:t1=0,t2=6
△t=6,小球从抛出至回落到地面所需要的时间是6秒.
A
【解析】试题分析:由小球高度h与运动时间t的关系式h=30t﹣5t2,令h=0,解得的两值之差便是所要求得的结果.
由小球高度h与运动时间t的关系式h=30t﹣5t2. 令h=0,﹣5t2+30t=0 解得:t1=0,t2=6
△t=6,小球从抛出至回落到地面所需要的时间是6秒. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 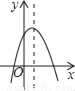 B.
B. 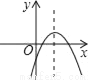 C.
C. 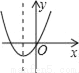 D.
D. 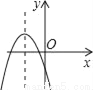
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 
