题目内容
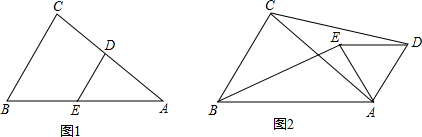
如图1,△ABC中,AB=AC,DE∥BC分别交AC、AB于D、E.
(1)求证:CD=BE;
(2)若将△ADE绕点A旋转一定的角度至图2的位置,那么CD=BE还成立吗?说明理由.
(1)求证:CD=BE;
(2)若将△ADE绕点A旋转一定的角度至图2的位置,那么CD=BE还成立吗?说明理由.

考点:平行线分线段成比例,全等三角形的判定与性质,旋转的性质
专题:
分析:(1)根据平行线截线段成比例证明CD=BE;
(2)利用全等三角形的判定定理SAS证得△ABE≌△ACD,然后根据全等三角形的对应边相等证得CD=BE.
(2)利用全等三角形的判定定理SAS证得△ABE≌△ACD,然后根据全等三角形的对应边相等证得CD=BE.
解答: (1)证明:如图1,∵DE∥BC,
(1)证明:如图1,∵DE∥BC,
∴
=
(平行线截线段成比例);
又∵AB=AC,
∴AD=AE,
∴AC-AD=AB-AE,即CD=BE;
(2)解:CD=BE还成立;
理由如下:∵△ADE绕点A旋转一定的角度至图2的位置,
∴∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD;
又由(1)知,AE=AD,
∴在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴CD=BE(全等三角形的对应边相等).
 (1)证明:如图1,∵DE∥BC,
(1)证明:如图1,∵DE∥BC,∴
| AD |
| AC |
| AE |
| AB |
又∵AB=AC,
∴AD=AE,
∴AC-AD=AB-AE,即CD=BE;
(2)解:CD=BE还成立;
理由如下:∵△ADE绕点A旋转一定的角度至图2的位置,
∴∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD;
又由(1)知,AE=AD,
∴在△ABE和△ACD中,
|
∴△ABE≌△ACD(SAS),
∴CD=BE(全等三角形的对应边相等).
点评:本题考查了平行线截线段成比例、全等三角形的判定与性质.注意利用平行线分线段成比例定理时,一定要找准对应关系,避免解答错误.

练习册系列答案
相关题目
2007年10月24日我国“嫦娥一号”探月卫星成功发射后,某航天科普网站的浏览量猛增.已知2007年10月份该网站的浏览量为80万人次,第四季度总浏览量为350万人次.如果浏览量平均每月增长率为x,则应列方程为( )
| A、80(1+x)2=350 |
| B、80+80×2x=350 |
| C、80+80×2(1+x)=350 |
| D、80[1+(1+x)+(1+x)2]=350 |
 已知在△ABC中,∠B=30°,tanC=2,AB=2,求△ABC的周长.(结果保留根号)
已知在△ABC中,∠B=30°,tanC=2,AB=2,求△ABC的周长.(结果保留根号) 如图,等腰△ABC中,AB=AC=10,AB的垂直平分线MN分别交AB于点M,AC于点N,△BCN的周长为16,那么BC=
如图,等腰△ABC中,AB=AC=10,AB的垂直平分线MN分别交AB于点M,AC于点N,△BCN的周长为16,那么BC= 如图,在△ABC中,EF∥BC,EF分别交边AB、AC于E、F两点,若AE=2,BE=4,则△AEF与△ABC的面积比为
如图,在△ABC中,EF∥BC,EF分别交边AB、AC于E、F两点,若AE=2,BE=4,则△AEF与△ABC的面积比为