题目内容
12.已知点G时△ABC的重心,$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{BC}$=$\overrightarrow{n}$,那么向量$\overrightarrow{AG}$用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示为$\frac{2}{3}$$\overrightarrow{m}$+$\frac{1}{3}$$\overrightarrow{n}$.分析 由点G时△ABC的重心,根据三角形重心的性质,即可求得$\overrightarrow{BD}$,再利用三角形法则求得$\overrightarrow{AD}$的长,继而求得答案.
解答  解:如图,
解:如图,
∵点G时△ABC的重心,$\overrightarrow{BC}$=$\overrightarrow{n}$,
∴$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{n}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{m}$+$\frac{1}{2}$$\overrightarrow{n}$,
∵点G时△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{m}$+$\frac{1}{3}$$\overrightarrow{n}$.
故答案为:$\frac{2}{3}$$\overrightarrow{m}$+$\frac{1}{3}$$\overrightarrow{n}$.
点评 此题考查了平面向量的知识与三角形重心的性质.注意掌握三角形法则的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.下列说法中,正确的个数有( )
①一组数据的平均数一定是该组数据中的某个数据;
②一组数据的中位数一定是该组数据中的某个数据;
③一组数据的众数一定是该组数据中的某个数据.
①一组数据的平均数一定是该组数据中的某个数据;
②一组数据的中位数一定是该组数据中的某个数据;
③一组数据的众数一定是该组数据中的某个数据.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.直线y=kx+b中,k<0,b<0,则直线不经过第( )象限.
| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
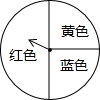 如图所示的一个转盘,小华认为转盘上共有三种不同的颜色,所以自由转动这个转盘两次,能配成紫色的概率为$\frac{2}{9}$,你认为小华说得正确吗?为什么?
如图所示的一个转盘,小华认为转盘上共有三种不同的颜色,所以自由转动这个转盘两次,能配成紫色的概率为$\frac{2}{9}$,你认为小华说得正确吗?为什么?