题目内容
16.对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数$\overline{abc}$(a≤c),在所有重新排列的三位数中,当|a+c-2b|最小时,称此时的$\overline{abc}$为t的“最优组合”,并规定F(t)=|a-b|-|b-c|,例如:124重新排序后为:142、214、因为|1+4-4|=1,|1+2-8|=5,|2+4-2|=4,所以124为124的“最优组合”,此时F(124)=-1.(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
分析 (1)由三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,根据“最优组合”的定义即可求解;
(2)由三位“善雅数”的定义,可得a为偶数,且2+x+y是3的倍数,且2+x+y<30,又由m的各位数字之和为一个完全平方数,可得2+x+y=32=9,继而求得答案.
解答 (1)证明:∵三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,
∴重新排序后:其中两个数位上数字的和是一个数位上的数字的2倍,
∴a+c-2b=0,
∴F(t)=0;
∵(2)∵m=200+10x+y是“善雅数”,
∴x为偶数,且2+x+y是3的倍数,
∵x<10,y<10,
∴2+x+y<30,
∵m的各位数字之和为一个完全平方数,
∴2+x+y=32=9,
∴当x=0时,y=7,
当x=2时,y=5,
当x=4时,y=3,
当x=6时,y=1,
∴所有符合条件的“善雅数”有:207,225,243,261,
∴所有符合条件的“善雅数”中F(m)的最大值是|2+7-0×2|=9.
点评 此题考查了完全平方数的应用问题.注意掌握数的整除问题,注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
相关题目
7.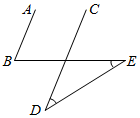 如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
11.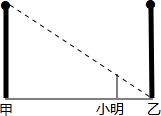 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
8.要使(x2+ax+1)(-6x3)的展开式中不含x4项,则a应等于( )
| A. | 6 | B. | -1 | C. | $\frac{1}{6}$ | D. | 0 |
5.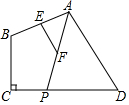 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )| A. | 线段EF的长先减小后增大 | B. | 线段EF的长不变 | ||
| C. | 线段EF的长逐渐增大 | D. | 线段EF的长逐渐减小 |