题目内容
20.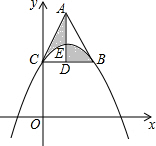 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
分析 根据抛物线y=a(x-3)2+k得到BC=2×3=6,根据是等边三角形的性质得到AD=3$\sqrt{3}$,于是得到结果.
解答 解:根据抛物线y=a(x-3)2+k得:BC=2×3=6,
∵△ABC是等边三角形,
∴AD=3$\sqrt{3}$,
根据二次函数图象的对称性得:S阴影=S△ABD=$\frac{1}{2}$×3×3$\sqrt{3}$=$\frac{9}{2}\sqrt{3}$,
故答案为:$\frac{9}{2}$$\sqrt{3}$.
点评 本题考查了二次函数的性质,等边三角形的性质,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
15.函数y=$\frac{k}{x}$的图象经过点(2,3),则k=( )
| A. | 2 | B. | 3 | C. | 6 | D. | -6 |
5.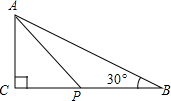 如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )
如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )
 如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )
如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )| A. | 2.5 | B. | 4.2 | C. | 5.8 | D. | 3.6 |
12.一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是( )
| A. | 360° | B. | 270° | C. | 180° | D. | 90° |
10.在一个不透明的口袋中装有5个质地、大小、颜色完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号不大于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |

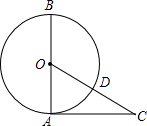 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)
如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)