题目内容
1.求不等式组$\left\{\begin{array}{l}{\frac{2x+1}{2}>-3}\\{1-2x>3}\end{array}\right.$的解集,并把解集在数轴上表示出来.分析 先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来斤.
解答 解:$\left\{\begin{array}{l}{\frac{2x+1}{2}>-3①}\\{1-2x>3②}\end{array}\right.$
∵由不等式①得:x>-$\frac{7}{2}$,
由不等式②得:x<-1,
∴不等式组的解集为-$\frac{7}{2}$<x<-1,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
12.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
11.把抛物线y=-x2向左平移2个单位,再向上平移3个单位,平移后的抛物线的解析式为( )
| A. | y=-(x-2)2-3 | B. | y=-(x+2)2-3 | C. | y=-(x+2)2+3 | D. | y=-(x-2)2+3 |
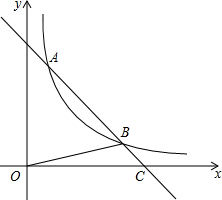 如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.
如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.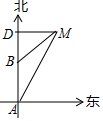 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°). 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)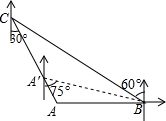 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.