题目内容
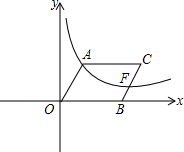 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,∠AOB=60°,反比例函数y=
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,∠AOB=60°,反比例函数y=| k |
| x |
| 3 |
考点:反比例函数综合题
专题:
分析:作AH⊥OB,FM⊥OB,设AH=a,设AH=a,由∠AOB=60°,可得AH,OH的值,由反比例函数y=
在第一象限经过点A,可得k的值,从而得出反比例函数的解析式,由四边形OACB是平行四边形,可得∠CBM=∠AOB,又由F为BC的中点,可得FM=
AH,由
a=
,可得x的值,从而得出OM,BM及OB的值,由S△AOF=S△OAB=
S平行四边形OACM,可得a的值,即可得出F的坐标.
| k |
| x |
| 1 |
| 2 |
| ||
| 4 |
| ||||
| x |
| 1 |
| 2 |
解答:解:如图,作AH⊥OB,FM⊥OB,

设AH=a,
∵∠AOB=60°,
∴AH=
a,OH=
a,
∵反比例函数y=
(k>0)在第一象限经过点A
∴
a=
,
∴k=
a2,
∴反比例函数y=
,
∵四边形OACB是平行四边形,
∴∠CBM=∠AOB=60°,
∵F为BC的中点,
∴FM=
AH=
a,
∴
a=
,解得x=a,
∴OM=a,BM=
a,
∴OB=OM-BM=a-
a=
a,
∵以A,O,F为顶点的三角形面积等于12
,
∴S△AOF=S△OAB=
S平行四边形OACM,
∴
×
a×
a=12
∴a=8,
∴F(
a,
a),即F(6,2
)
故答案为(6,2
).

设AH=a,
∵∠AOB=60°,
∴AH=
| ||
| 2 |
| 1 |
| 2 |
∵反比例函数y=
| k |
| x |
∴
| ||
| 2 |
| k | ||
|
∴k=
| ||
| 4 |
∴反比例函数y=
| ||||
| x |
∵四边形OACB是平行四边形,
∴∠CBM=∠AOB=60°,
∵F为BC的中点,
∴FM=
| 1 |
| 2 |
| ||
| 4 |
∴
| ||
| 4 |
| ||||
| x |
∴OM=a,BM=
| 1 |
| 4 |
∴OB=OM-BM=a-
| 1 |
| 4 |
| 3 |
| 4 |
∵以A,O,F为顶点的三角形面积等于12
| 3 |
∴S△AOF=S△OAB=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| 3 |
∴a=8,
∴F(
| 3 |
| 4 |
| ||
| 4 |
| 3 |
故答案为(6,2
| 3 |
点评:本题主要考查了反比例函数综合题,解题的关键是正确作出辅助线,求出OA的长度.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
一个数是8,另一个数比8的相反数小3,则这两个数的和为( )
| A、-3 | B、-19 | C、19 | D、3 |
已知m2+2mn=13,3mn+2n2=21,则2m2+13mn+6n2-44的值为( )
| A、45 | B、5 | C、66 | D、77 |
若分式
=0,则a取值为( )
| a2-4 |
| a-2 |
| A、a=2 | B、a=-2 |
| C、a=0 | D、a=-2或a=2 |
下列计算错误的是( )
A、a(a-
| ||||
| B、(a-2)2=a2-4a+4 | ||||
| C、(a2-2ab+a)÷a=a-2b+1 | ||||
| D、(a+2)(a-3)=a2-6 |

 尺规作图(不写作法,保留作图痕迹)
尺规作图(不写作法,保留作图痕迹)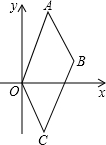 如图,在平面直角坐标系中,A(1,3)、B(2,1),四边形ABCD是平行四边形,求点C的坐标.
如图,在平面直角坐标系中,A(1,3)、B(2,1),四边形ABCD是平行四边形,求点C的坐标.