题目内容
已知m2+2mn=13，3mn+2n2=21，则2m2+13mn+6n2-44的值为（ ）
| A、45 | B、5 | C、66 | D、77 |
考点：整式的加减—化简求值
专题：计算题
分析：已知第一个等式两边乘以2，第二个等式两边乘以3，两式相加即可得到结果．
解答：解：已知等式变形得：2m2+4mn=26，9mn+6n2=63，
两式相加得：2m2+13mn+6n2=89，
则原式=89-44=45．
故选A．
两式相加得：2m2+13mn+6n2=89，
则原式=89-44=45．
故选A．
点评：此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
下列各组数中互为相反数的是（ ）
A、3和
| |||
B、-
| |||
C、-3和
| |||
| D、-|-3|和-（-3） |
若关于x的方程（a-3）x2-2x+1=0有实数根，则a满足（ ）
| A、a≤4 |
| B、a≤4且a≠3 |
| C、a＜4且a≠3 |
| D、a≠3 |
若正比例函数y=kx经过点（1，2），则反比例函数y=
，下列说法不正确的是（ ）
| k |
| x |
| A、点（-2，-1）在它的图象上 |
| B、它的图象在第一、三象限 |
| C、当x＞0时，y随x的增大而增大 |
| D、当x＜0时，y随x的增大而减小 |
如果把
的x与y都扩大10倍，那么这个代数式的值（ ）
| 2x |
| x-y |
| A、不变 | ||
| B、扩大20倍 | ||
| C、扩大10倍 | ||
D、缩小到原来的
|
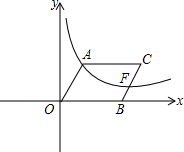如图，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，∠AOB=60°，反比例函数y=
如图，抛物线y=ax2+bx+4的对称轴是直线x=