题目内容
如图,在平面直角坐标系中,O为坐标原点,直线y=-x+6交y轴于点A,交x轴于点B,点C,B关于原点对称,点P在射线AB上运动,连接CP与y轴交于点D,连接BD,过P,D,B三点作⊙Q与y轴的另一个交点E,延长DQ交⊙Q于点F,连接EF,BF.
(1)求A,B,C三点的坐标;
(2)当点P在线段AB(不包括A,B两点)上时,求证:DE=EF;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标;如果不存在,请说明理由.

(1)求A,B,C三点的坐标;
(2)当点P在线段AB(不包括A,B两点)上时,求证:DE=EF;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标;如果不存在,请说明理由.

考点:圆的综合题
专题:
分析:(1)由直线y=-x+6交y轴于点A,交x轴于点B,当x=0时,y=6,当y=0时,x=6,即可得A,B的坐标,再由点C,B关于原点对称,即可求出点C的坐标,
(2)先证出△BDO≌△COD,得出∠BDO=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP,再连结PE,根据∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,∠ADP=∠BDE,∠DEP=∠ABD,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,最后根据∠DEF=90°,得出△DEF是等腰直角三角形,从而求出DE=EF,
(3)BD:BF=2:1时,过点F作FH⊥OB于点H,证出△BOD∽△FHB=2,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4OD,根据DE=EF,求出OD的长,从而得出直线CD的解析式,最后根求出点P的坐标即可;连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB,得出FG,ODBG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根即可求出点P的坐标.
(2)先证出△BDO≌△COD,得出∠BDO=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP,再连结PE,根据∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,∠ADP=∠BDE,∠DEP=∠ABD,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,最后根据∠DEF=90°,得出△DEF是等腰直角三角形,从而求出DE=EF,
(3)BD:BF=2:1时,过点F作FH⊥OB于点H,证出△BOD∽△FHB=2,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4OD,根据DE=EF,求出OD的长,从而得出直线CD的解析式,最后根求出点P的坐标即可;连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB,得出FG,ODBG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根即可求出点P的坐标.
解答:解:(1)∵直线y=-x+6交y轴于点A,交x轴于点B,
∴当x=0时,y=6,
当y=0时,x=6,
∴A(0,6),B(6,0)
∵点C,B关于原点对称,
∴C(-6,0),
(2)①由已知得:OB=OC,∠BOD=∠COD=90°,
又∵OD=OD,
∴△BDO≌△CDO,
∴∠BDO=∠CDO,
∵∠CDO=∠ADP,
∴∠BDE=∠ADP,
如图1,连结PE,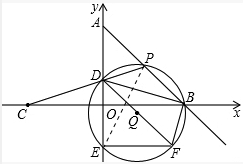
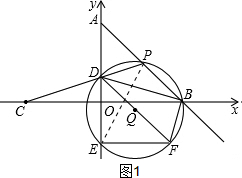
∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∵OA=OB=6,∠AOB=90°,
∴∠OAB=45°,
∴∠DPE=45°,
∴∠DFE=∠DPE=45°,
∵DF是⊙Q的直径,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∴DE=EF,
(3)当BD:BF=2:1时,
①如图2,过点F作FH⊥OB于点H,
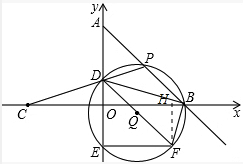
∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,
∴∠DBO=∠BFH,
又∵∠DOB=∠BHF=90°,
∴△BOD∽△FHB,
∴
=
=
=2,
∴FH=3,OD=2BH,
∵∠FHO=∠EOH=∠OEF=90°,
∴四边形OEFH是矩形,
∴OE=FH=3,
∴EF=OH=6-
OD,
∵DE=EF,
∴3+OD=6-
OD,
解得:OD=2,
∴点D的坐标为(0,2),
∴直线CD的解析式为y=
x+2,
由
,解得
,
则点P的坐标为(3,3);
当
=
时,
②如图3,连结EB,同(2)可得:∠ADB=∠EDP,
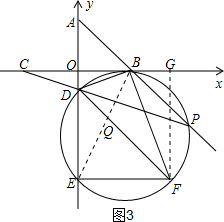
而∠ADB=∠DEB+∠DBE,∠EDP=∠DAP+∠DPA,
∵∠DEB=∠DPA,
∴∠DBE=∠DAP=45°,
∴△DEF是等腰直角三角形,过点F作FG⊥OB于点G,
同理可得:△BOD∽△FGB,
∴
=
=
=
,
∴FG=12,OD=
BG,
∵∠FGO=∠GOE=∠OEF=90°,
∴四边形OEFG是矩形,
∴OE=FG=12
∴EF=OG=6+2OD,
∵DE=EF,
∴12-OD=6+2OD,
OD=2
∴点D的坐标为(0,-2)
直线CD的解析式为:y=-
x-2,
由
得
∴点P的坐标为(12,-6),
综上所述,点P的坐标为(3,3)或(12,-6).
∴当x=0时,y=6,
当y=0时,x=6,
∴A(0,6),B(6,0)
∵点C,B关于原点对称,
∴C(-6,0),
(2)①由已知得:OB=OC,∠BOD=∠COD=90°,
又∵OD=OD,
∴△BDO≌△CDO,
∴∠BDO=∠CDO,
∵∠CDO=∠ADP,
∴∠BDE=∠ADP,
如图1,连结PE,


∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∵OA=OB=6,∠AOB=90°,
∴∠OAB=45°,
∴∠DPE=45°,
∴∠DFE=∠DPE=45°,
∵DF是⊙Q的直径,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∴DE=EF,
(3)当BD:BF=2:1时,
①如图2,过点F作FH⊥OB于点H,

∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,
∴∠DBO=∠BFH,
又∵∠DOB=∠BHF=90°,
∴△BOD∽△FHB,
∴
| OB |
| HF |
| OD |
| HB |
| BD |
| FB |
∴FH=3,OD=2BH,
∵∠FHO=∠EOH=∠OEF=90°,
∴四边形OEFH是矩形,
∴OE=FH=3,
∴EF=OH=6-
| 1 |
| 2 |
∵DE=EF,
∴3+OD=6-
| 1 |
| 2 |
解得:OD=2,
∴点D的坐标为(0,2),
∴直线CD的解析式为y=
| 1 |
| 3 |
由
|
|
则点P的坐标为(3,3);
当
| BD |
| BF |
| 1 |
| 2 |
②如图3,连结EB,同(2)可得:∠ADB=∠EDP,

而∠ADB=∠DEB+∠DBE,∠EDP=∠DAP+∠DPA,
∵∠DEB=∠DPA,
∴∠DBE=∠DAP=45°,
∴△DEF是等腰直角三角形,过点F作FG⊥OB于点G,
同理可得:△BOD∽△FGB,
∴
| OB |
| GF |
| OD |
| GB |
| BD |
| FB |
| 1 |
| 2 |
∴FG=12,OD=
| 1 |
| 2 |
∵∠FGO=∠GOE=∠OEF=90°,
∴四边形OEFG是矩形,
∴OE=FG=12
∴EF=OG=6+2OD,
∵DE=EF,
∴12-OD=6+2OD,
OD=2
∴点D的坐标为(0,-2)
直线CD的解析式为:y=-
| 1 |
| 3 |
由
|
|
∴点P的坐标为(12,-6),
综上所述,点P的坐标为(3,3)或(12,-6).
点评:此题主要考查了圆的综合,用到的知识点是一次函数、矩形的性质、圆的性质,关键是综合运用有关知识作出辅助线,列出方程组.

练习册系列答案
相关题目
若方程(a2-1)x2+(a-1)x+(2a+1)y=0是二元一次方程,则a的值为( )
| A、1 | B、-1 | C、±1 | D、一切实数 |
为了响应中央号召,2012年某市加大财政支农力度,全市农业支出累计约达到53000万元,其中53000万元(保留三位有效数字)用科学记数法可表示为( )
| A、5.3×107元 |
| B、5.30×107元 |
| C、530×108元 |
| D、5.30×108元 |
若关于x的方程(a-3)x2-2x+1=0有实数根,则a满足( )
| A、a≤4 |
| B、a≤4且a≠3 |
| C、a<4且a≠3 |
| D、a≠3 |
若正比例函数y=kx经过点(1,2),则反比例函数y=
,下列说法不正确的是( )
| k |
| x |
| A、点(-2,-1)在它的图象上 |
| B、它的图象在第一、三象限 |
| C、当x>0时,y随x的增大而增大 |
| D、当x<0时,y随x的增大而减小 |
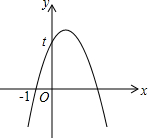 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).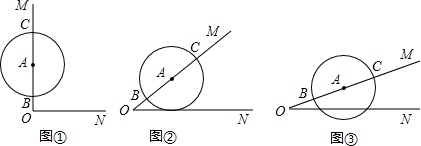
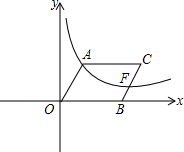 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,∠AOB=60°,反比例函数y=
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,∠AOB=60°,反比例函数y=