题目内容
10.先化简,再求值:$\frac{x}{{x}^{2}-1}$÷(1+$\frac{1}{x-1}$),其中x=-$\frac{2}{3}$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{x-1}$=$\frac{x}{(x+1)(x-1)}$•$\frac{x-1}{x}$=$\frac{1}{x+1}$,
当x=-$\frac{2}{3}$时,原式=3.
点评 此题考查了分式的化简求值,熟练掌握通分及约分是解本题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
1.-2017的绝对值是( )
| A. | $\frac{1}{2017}$ | B. | ±2017 | C. | 2017 | D. | -2017 |
15.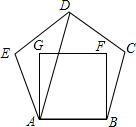 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )| A. | 30 | B. | 28 | C. | 20 | D. | 18 |
19.下列等式变形正确的是( )
| A. | 由a=b,得$\frac{a}{-4}$=$\frac{b}{-4}$ | B. | 由-3x=-3y,得x=-y | ||
| C. | 由$\frac{x}{4}$=1,得x=$\frac{1}{4}$ | D. | 由x=y,得$\frac{x}{a}$=$\frac{y}{a}$ |
20.弧长为6π的弧所对的圆心角为60°,则弧所在的圆的半径为( )
| A. | 6 | B. | 6 $\sqrt{3}$ | C. | 12 $\sqrt{3}$ | D. | 18 |

 如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.