题目内容
8.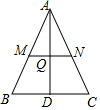 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=BC=1.点Q是AD上的一个动点,过点Q垂直于AD的直线分别交AB、AC于M、N两点,设AQ=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=BC=1.点Q是AD上的一个动点,过点Q垂直于AD的直线分别交AB、AC于M、N两点,设AQ=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )| A. | 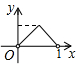 | B. | 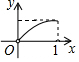 | C. | 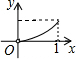 | D. | 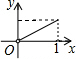 |
分析 根据相似三角形的判定与性质,可得MN与AQ,的关系,根据三角形的面积,可得答案.
解答 解:由AD⊥BC,AQ⊥MN,
得△AMN∽△ABC,
$\frac{AQ}{QD}$=$\frac{MN}{BC}$,AD=BC,
得AQ=MN,
S△AMN=$\frac{1}{2}$AQ•MN=$\frac{1}{2}$AQ2,
即y=$\frac{1}{2}$x2,
由0<AQ<1,
得0<x<1,
故选:C.
点评 本题考查了动点问题的函数图象,利用相似三角形的判定与性质得出AQ=MN是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
18.若式子$\sqrt{k-1}$+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.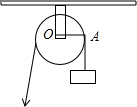 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )| A. | 5πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
16.下列说法错误的是( )
| A. | 斜边及一锐角分别相等的两个直角三角形全等 | |
| B. | 两条直角边分别相等的两个直角三角形全等 | |
| C. | 两个锐角分别相等的两个直角三角形全等 | |
| D. | 一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等 |
20.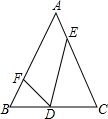 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3.5 |
17. 把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )
把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )
 把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )
把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )| A. | 祝 | B. | 试 | C. | 顺 | D. | 利 |
 如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?
如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?