题目内容
6.如图1,在直角三角形ABC中,∠A=90°,点D在线段BC上,∠EDC=$\frac{1}{2}$∠B,CE⊥DE,垂足为E,DE与AC相交于点F.(1)当$\frac{AC}{AB}=1$时(如图2),作DG∥BA,交AC于H,交CE延长线于点G.
①∠ECF=22.5°;
②通过证明△CED≌△GED与△CGH≌△DFH,可得$\frac{CE}{FD}=\frac{1}{2}$,请说明这一推理过程.
(2)当$\frac{AC}{AB}=3$时(如图3),证明:$\frac{CE}{FD}=\frac{3}{2}$.

分析 (1)①根据等腰直角三角形的性质得到∠B=45°,根据角平分线的定义得到∠GDE=22.5°,根据同角的余角相等得到答案;
②证明△CED≌△GED和△CGH≌△DFH,根据全等三角形的性质证明结论;
(2)根据AC=3AB,结合②的结论,得到答案.
解答 解:(1)①∵∠A=90°,$\frac{AC}{AB}=1$,
∴∠B=45°,
∵DG∥BA,∴∠GDC=∠B=45°,
∵∠EDC=$\frac{1}{2}$∠B=22.5°,∴∠GDE=22.5°,
∵∠DHF=∠DEC=90°,
∴∠ECF=22.5;
②证明如下:
∵DG∥AB,∠EDC=$\frac{1}{2}$∠B,
∴∠EDC=∠GDE,又∵CE⊥DE,
∴∠CED=∠GED=90°,
在△CED和△GED中,
$\left\{\begin{array}{l}{∠GDE=∠CDE}\\{∠DEG=∠DEC}\\{DE=DE}\end{array}\right.$,
∴△CED≌△GED,
∴CE=GE,即$CE=\frac{1}{2}CG$,
∵DG∥AB,∠A=90°,AB=AC,
∴∠CHG=∠DHF=90°,CH=DH.
又∵∠GCH=∠FDH,
∴△CGH≌△DFH,
∴CG=FD.
∴$CE=\frac{1}{2}FD$;
(2)作DG∥BA,交AC于H,交CE延长线于点G,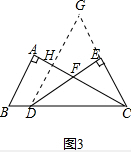
同(1)可证$CE=\frac{1}{2}CG$.
∵DG∥AB,
∴∠DHF=∠CHG=90°,又∵∠GCH=∠FDH,
∴△CGH∽△DFH,
∴$\frac{CG}{FD}=\frac{CH}{DH}$
∵DG∥AB,
∴△CHD∽△CAB,
∴$\frac{CH}{DH}=\frac{AC}{AB}=3$,
∴$\frac{CG}{FD}=3$,∴$\frac{2CE}{FD}$=3,即$\frac{CE}{FD}=\frac{3}{2}$.
点评 本题考查的是相似三角形的性质、全等三角形的判定和性质以及平行线的性质,正确作出辅助线、灵活运用相关定理和性质是解题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?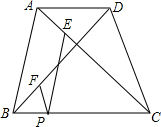 如图,梯形ABCD中,AD∥BC AB=DC=3,P是BC上一点,PE∥AB交AC于E,PF∥CD交BD于F,若PE、PF的长分别为m、n,设x=m+n,当点P在BC上移动时,x的值是否变化?若变化,求出x的取值范围.若不变,求出x的值.
如图,梯形ABCD中,AD∥BC AB=DC=3,P是BC上一点,PE∥AB交AC于E,PF∥CD交BD于F,若PE、PF的长分别为m、n,设x=m+n,当点P在BC上移动时,x的值是否变化?若变化,求出x的取值范围.若不变,求出x的值. 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.