题目内容
18. 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
分析 首先连接OA,O1F,过点O作OE⊥AB于点E,由垂径定理即可求得AE=BE,又由大半圆的弦AB与小半圆相切于F,且AB∥CD,可得O1F=OE,继而可得S阴影=S大半圆-S小半圆=$\frac{1}{2}$π(OA2-EO2).
解答 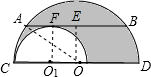 解:连接OA,O1F,过点O作OE⊥AB于点E,
解:连接OA,O1F,过点O作OE⊥AB于点E,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2(cm),
∵大半圆的弦AB与小半圆相切于F,
∴O1F⊥AB,
∵AB∥CD,
∴O1F=OE,
由勾股定理知,OA2-EO2=AE2=4,
∴S阴影=S大半圆-S小半圆=$\frac{1}{2}$π(OA2-EO2)=2π(cm2).
点评 此题考查了切线的性质以及垂径定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
7.某公司对员工的月收入统计如表:
由于公司的效益不断提高,公司领导决定提高员工的月收入,提高后员工的月收入情况如表:
(1)求该公司员工原平均月收入和提高后的平均月收入;
(2)员工收入提高后,该公司每月需要多拿出多少元支付员工的月收入?
| 收入x (单位:元) | 600≤x <1000 | 1000≤x <1400 | 1400≤x <1800 |
| 人数 | 12 | 50 | 18 |
| 收入x (单位:元) | 1000≤x <1400 | 1400≤x <1800 | 1800≤x <2200 |
| 人数 | 12 | 50 | 18 |
(2)员工收入提高后,该公司每月需要多拿出多少元支付员工的月收入?

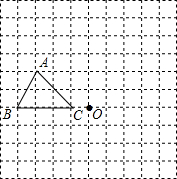 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上. 如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,AD=5,AB=4,求CE的长.
如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,AD=5,AB=4,求CE的长.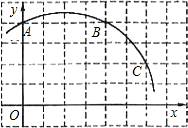 如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).
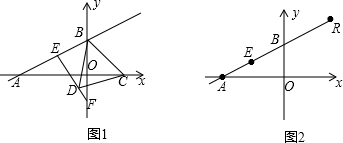
如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2). 如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.