题目内容
18. 如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
分析 首先根据勾股定理得出AC的长,再利用勾股定理定理得出△DAC是直角三角形,结合四边形ABCD的面积为:S△DAC-S△ABC求出即可.
解答  解:连接AC,
解:连接AC,
∵∠ABC=90°,AB=4m,BC=3m,
∴AC=5m,
∵CD=13m,AD=12m,
∴AC2+AD2=CD2,
∴△DAC是直角三角形,
∴S△DAC=$\frac{1}{2}$×AD×AC=$\frac{1}{2}$×12×5=30(m2),
∴四边形ABCD的面积为:S△DAC-S△ABC=30-$\frac{1}{2}$×3×4=24(m2).
点评 此题主要考查了勾股定理以及勾股定理的逆定理,得出△DAC是直角三角形是解题关键.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 16的平方根是4 | B. | -1的平方根是-1 | ||
| C. | -2是4的一个平方根 | D. | (-1)2的平方根是-1 |
 如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
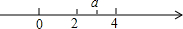 实数a在数轴上的位置如图所示,化简|a-2|+$\sqrt{{a}^{2}-8a+16}$=2.
实数a在数轴上的位置如图所示,化简|a-2|+$\sqrt{{a}^{2}-8a+16}$=2.
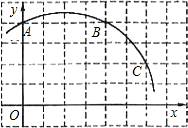 如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).
如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).