题目内容
2. 已知,如图,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AB=CE,则不正确的结论是( )
已知,如图,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AB=CE,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠1=∠2 |
分析 根据HL证Rt△ABC≌Rt△CED,根据全等三角形的性质即可求出答案.
解答 解:∵∠B=∠E=90°,
∴在Rt△ABC和Rt△CED中
$\left\{\begin{array}{l}{AC=CD}\\{AB=CE}\end{array}\right.$,
∴Rt△ABC≌Rt△CED(HL),故C正确,
∴∠A=∠2,∠1=∠D,
∵∠1+∠A=90°,
∴∠A+∠D=90°,∠1+∠2=90°,
∴∠A与∠D互为余角,故A、B正确;D 错误,
故选D.
点评 本题考查了全等三角形的性质和判定,关键是推出Rt△ABC≌Rt△CED.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知sinB=$\frac{\sqrt{2}}{2}$,则∠B等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.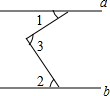 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )| A. | 100° | B. | 90° | C. | 70° | D. | 50° |
17.若(a2+b2-5)2=25,则a2+b2=( )
| A. | 8或-2 | B. | -2 | C. | 8 | D. | 0或10 |
 如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?
如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?