题目内容
13．已知sinB=$\frac{\sqrt{2}}{2}$，则∠B等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 直接根据特殊角的三角函数值进行解答即可．
解答 解：∵sin45°=$\frac{\sqrt{2}}{2}$，
∴∠B=45°．
故选B．
点评 本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．
练习册系列答案
相关题目
12．
如图，数轴上与1，$\sqrt{2}$对应的点分别为A，B，点B关于点A的对称点为C，设点C表示的数为x，则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是（ ）
如图，数轴上与1，$\sqrt{2}$对应的点分别为A，B，点B关于点A的对称点为C，设点C表示的数为x，则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是（ ）| A． | $\sqrt{2}-3$ | B． | 2$\sqrt{2}$-1 | C． | 3$\sqrt{2}$-3 | D． | 2-$\sqrt{2}$ |
5．
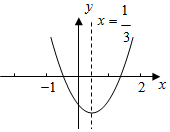如图所示的二次函数 y=ax2+bx+c 的图象中，观察得出了下面五条信息：
①c＜0；②abc＞0；
③a+b+c＞0；④2a-3b=0；
⑤c-4b＞0．
其中正确信息是（ ）
如图所示的二次函数 y=ax2+bx+c 的图象中，观察得出了下面五条信息：①c＜0；②abc＞0；
③a+b+c＞0；④2a-3b=0；
⑤c-4b＞0．
其中正确信息是（ ）
| A． | ①②③ | B． | ①②④ | C． | ①②⑤ | D． | ①②③④ |
2．
已知，如图，B、C、E三点在同一条直线上，AC=CD，∠B=∠E=90°，AB=CE，则不正确的结论是（ ）
已知，如图，B、C、E三点在同一条直线上，AC=CD，∠B=∠E=90°，AB=CE，则不正确的结论是（ ）| A． | ∠A与∠D互为余角 | B． | ∠A=∠2 | C． | △ABC≌△CED | D． | ∠1=∠2 |