Question

11．在平面直角坐标系xOy中，抛物线C：y=x²+（3-m）x经过点A（-1，0）．
（1）求抛物线C的表达式；
（2）将抛物线C沿直线y=1翻折，得到的新抛物线记为C₁，求抛物线C₁的顶点坐标；
（3）将抛物线C沿直线y=n翻折，得到的图象记为C₂，设C与C₂围成的封闭图形为M，在图形M上内接一个面积为4的正方形（四个顶点均在M上），且这个正方形的边分别与坐标轴平行．求n的值．

Answer 1

分析 （1）把点A（-1，0）代入y=x²+（3-m）x，根据待定系数法即可求得．
（2）把抛物线C的表达式化成顶点式，求得顶点P的坐标，然后求得关于直线y=1的对称点P′的坐标，即为抛物线C₁的顶点坐标；
（3）由抛物线C的顶点式求得对称轴，然后根据正方形的边长求得B的坐标，进而得出$n-\frac{3}{4}=1$，解得n=$\frac{7}{4}$．

解答 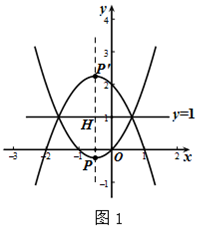解：（1）∵抛物线C：y=x²+（3-m）x经过点A（-1，0），
∴1-（3-m）=0．
∴m=2．
∴抛物线C的表达式为y=x²+x．

（2）∵抛物线C：y=x²+x=（x+$\frac{1}{2}$）²-$\frac{1}{4}$，
∴抛物线C的顶点为$P（-\frac{1}{2}，-\frac{1}{4}）$，如图1，
点$P（-\frac{1}{2}，-\frac{1}{4}）$关于直线y=1的对称点为P'$（-\frac{1}{2}，\frac{9}{4}）$．
∴抛物线C₁的顶点坐标为$（-\frac{1}{2}，\frac{9}{4}）$．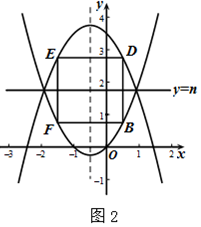

（3）∵抛物线C：y=x²+x=（x+$\frac{1}{2}$）²-$\frac{1}{4}$，
∴抛物线的对称轴为$x=-\frac{1}{2}$，
∵正方形的边长为2，
∴正方形的顶点B的坐标为$（\frac{1}{2}，\frac{3}{4}）$，如图2．
∴$n-\frac{3}{4}=1$．
∴$n=\frac{7}{4}$．

点评 本题考查了待定系数法求二次函数的解析式以及二次函数的图象与几何变换，熟练掌握轴对称的性质、正方形的性质是解题的关键．