题目内容
计算:
(1)(-
a5b2)3;
(2)(-x)3÷x•(-x)2;
(3)-102n×100÷(-10)2n-1;
(4)(-9)3×(-
)3×(
)3.
(1)(-
| 1 |
| 2 |
(2)(-x)3÷x•(-x)2;
(3)-102n×100÷(-10)2n-1;
(4)(-9)3×(-
| 2 |
| 3 |
| 1 |
| 3 |
考点:同底数幂的除法,同底数幂的乘法,幂的乘方与积的乘方
专题:计算题
分析:(1)根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘进行计算即可得解;
(2)根据同底数幂相除,底数不变指数相减,同底数幂相乘,底数不变指数相加进行计算即可得解;
(3)先转化为以10为底数的幂的运算,再根据同底数幂相除,底数不变指数相减,同底数幂相乘,底数不变指数相加进行计算即可得解;
(4)根据积的乘方的性质的逆运用进行计算即可得解.
(2)根据同底数幂相除,底数不变指数相减,同底数幂相乘,底数不变指数相加进行计算即可得解;
(3)先转化为以10为底数的幂的运算,再根据同底数幂相除,底数不变指数相减,同底数幂相乘,底数不变指数相加进行计算即可得解;
(4)根据积的乘方的性质的逆运用进行计算即可得解.
解答:解:(1)(-
a5b2)3=-
a15b6;
(2)(-x)3÷x•(-x)2,
=-x3÷x•x2,
=-x3-1+2,
=-x2;
(3)-102n×100÷(-10)2n-1,
=-102n×102÷(-102n-1),
=102n+2-2n+1,
=103,
=1000;
(4)(-9)3×(-
)3×(
)3,
=[(-9)×(-
)×(
)]3,
=23,
=8.
| 1 |
| 2 |
| 1 |
| 8 |
(2)(-x)3÷x•(-x)2,
=-x3÷x•x2,
=-x3-1+2,
=-x2;
(3)-102n×100÷(-10)2n-1,
=-102n×102÷(-102n-1),
=102n+2-2n+1,
=103,
=1000;
(4)(-9)3×(-
| 2 |
| 3 |
| 1 |
| 3 |
=[(-9)×(-
| 2 |
| 3 |
| 1 |
| 3 |
=23,
=8.
点评:本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方的性质,熟记性质并理清指数的变化是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
等腰三角形的顶角A=120°,底边BC的长为12cm,那么它的腰长是( )
A、2
| ||
B、4
| ||
C、
| ||
| D、6cm |
 如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.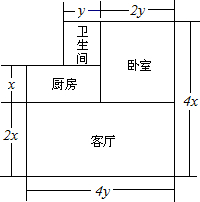 一住宅的结构如图,主人打算把卧室以外的部分铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是每平方米a元,那么购买所需的地砖至少需要多少元?
一住宅的结构如图,主人打算把卧室以外的部分铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格是每平方米a元,那么购买所需的地砖至少需要多少元? 如图,某商场工作人员要在大厅安装一部电梯,已知一、二楼层高3.4m,可供电梯伸展的地面长度不超过10m.求电梯的最小倾斜角(精确到0.01°).
如图,某商场工作人员要在大厅安装一部电梯,已知一、二楼层高3.4m,可供电梯伸展的地面长度不超过10m.求电梯的最小倾斜角(精确到0.01°). 如图,在四边形ABCD中,AB∥CD,要在边AB上找一点E,使∠AEC=150°,应怎样确定点E的位置?为什么?
如图,在四边形ABCD中,AB∥CD,要在边AB上找一点E,使∠AEC=150°,应怎样确定点E的位置?为什么? 如图,GH分别交AB、CD于点E、F,∠AEF=∠EFD.
如图,GH分别交AB、CD于点E、F,∠AEF=∠EFD.