题目内容
8.△ABC中,点D、E分别是AB、AC的中点,则下列的结论:①△ADE∽△ABC;②$\frac{DE}{BC}$=$\frac{AE}{AC}$;③$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{2}$;④$\frac{DE}{BC}$=$\frac{AD}{BD}$,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据中位线定理得到DE∥BC,根据相似三角形的判定定理判断①;
根据相似三角形的性质判断②;
根据相似三角形的面积比等于相似比的平方判断③;
根据相似三角形的性质定理判断④.
解答 解:∵点D、E分别是AB、AC的中点,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,①正确;
$\frac{DE}{BC}$=$\frac{AE}{AC}$,②正确;
$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{4}$,③错误;
$\frac{DE}{BC}$=$\frac{AD}{AB}$,④错误,
故选:C.
点评 本题考查的是三角形中位线定理和相似三角形的性质和判定,掌握三角形的中位线平行于第三边且等于第三边的一半、相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
20.下列命题中,正确的是( )
| A. | 平面上三个点确定一个圆 | |
| B. | 与某圆一条半径垂直的直线是该圆的切线 | |
| C. | 三角形的外心在三角形的外面 | |
| D. | 等弧所对的圆周角相等 |
18.下列调查中,比较适合普查方式的是( )
| A. | 对端午节市场上粽子质量情况的调查 | |
| B. | 对神舟九号载人飞船各零部件的质量的调查 | |
| C. | 调查全国中学生每天体育锻炼的时间 | |
| D. | 为了解我市市民实施低碳生活的情况 |
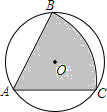 如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$.
如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$.
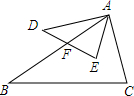 如图,已知△ABC与△ADE中,则∠C=∠E,∠DAB=∠CAE,∠D=∠B,$\frac{AF}{AC}$=$\frac{AD}{AB}$,$\frac{DE}{BC}$=$\frac{AE}{AC}$,$\frac{AD}{AE}$=$\frac{AB}{AC}$,则下列各式成立的个数是( )
如图,已知△ABC与△ADE中,则∠C=∠E,∠DAB=∠CAE,∠D=∠B,$\frac{AF}{AC}$=$\frac{AD}{AB}$,$\frac{DE}{BC}$=$\frac{AE}{AC}$,$\frac{AD}{AE}$=$\frac{AB}{AC}$,则下列各式成立的个数是( )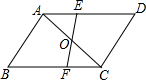 如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.
如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F. 如图,抛物线y=-x2+bx+c与x轴交于点A(-3,0),B(1,0)(点A在点B的左边),与y轴交于点C,点D是线段AB上一动点,过点D作DE⊥x轴,交直线AC于点E,交抛物线于点F.设点D的横坐标为m,线段EF的长为d.
如图,抛物线y=-x2+bx+c与x轴交于点A(-3,0),B(1,0)(点A在点B的左边),与y轴交于点C,点D是线段AB上一动点,过点D作DE⊥x轴,交直线AC于点E,交抛物线于点F.设点D的横坐标为m,线段EF的长为d.