如图.已知△ABC与△ADE中.则∠C=∠E.∠DAB=∠CAE.∠D=∠B.$\frac{AF}{AC}$=$\frac{AD}{AB}$.$\frac{DE}{BC}$=$\frac{AE}{AC}$.$\frac{AD}{AE}$=$\frac{AB}{AC}$.则下列各式成立的个数是( )A．1个B．2个C．3个D．4个题目和参考答案——青夏教育精英家教网—

题目内容

16．

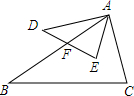如图，已知△ABC与△ADE中，则∠C=∠E，∠DAB=∠CAE，∠D=∠B，$\frac{AF}{AC}$=$\frac{AD}{AB}$，$\frac{DE}{BC}$=$\frac{AE}{AC}$，$\frac{AD}{AE}$=$\frac{AB}{AC}$，则下列各式成立的个数是（　　）

A．

1个

B．

2个

C．

3个

D．

4个

分析证明△ABC∽△ADE，得出对应边成比例$\frac{DE}{BC}$=$\frac{AE}{AC}$，$\frac{AD}{AE}$=$\frac{AB}{AC}$，即可得出结果．

解答解：∵∠C=∠E，∠D=∠B，
∴△ABC∽△ADE，
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$，$\frac{AD}{AE}$=$\frac{AB}{AC}$，
∴成立的个数有2个，
故选：B．

点评本题考查了相似三角形的判定与性质；熟练掌握相似三角形的判定与性质，并能进行推理论证是解决问题的关键．

练习册系列答案

相关题目

6．

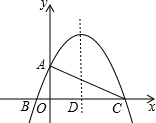如图，已知二次函数y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．
（1）点A的坐标为（0，4），点C的坐标为（8，0）；
（2）线段AC上是否存在点E，使得△EDC为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由．

7．若分式$\frac{-{x}^{2}}{1-5x}$的值是负数，则x的取值范围为x＜$\frac{1}{5}$且x≠0．

4．直角三角形中，有三点A（2，0）、B（-3，-4）、O（0，0），则△AOB的面积为（　　）

11．

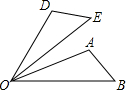如图，△AOB绕点O旋转到△DOE的位置，请指出旋转角．
小明的解答是：因为△DOE是由△AOB绕点O旋转得到的，所以∠DOE，∠AOB，∠EOA就是旋转角，小明的解答对吗？若不对，请给出正确答案．

1．已知二次函数y=x²-5x+m（m为实数）的图象与x轴上的一个交点为（2，0），则关于x的一元二次方程x²-5x+m=0的两实数根是（　　）

x₁=2，x₂=-2

x₁=2，x₂=3

x₁=2，x₂=0

x₁=2，x₂=-3

8．△ABC中，点D、E分别是AB、AC的中点，则下列的结论：①△ADE∽△ABC；②$\frac{DE}{BC}$=$\frac{AE}{AC}$；③$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{2}$；④$\frac{DE}{BC}$=$\frac{AD}{BD}$，其中正确的有（　　）

5．已知直线y=x-3与x轴、y轴交于A、B两点，抛物线y=ax²+bx+c经过点A、B及点E（-2，5）．
（1）求此抛物线的解析式及顶点M的坐标；
（2）设此抛物线与x轴另一交点为C，求四边形AMBC的面积．

6．解方程：2x²+x-6=0．

试题分类