题目内容
5.计算:(1)($\sqrt{6}$-$\frac{1}{3}$$\sqrt{\frac{3}{2}}$-$\frac{1}{2}$$\sqrt{24}$)×(-2$\sqrt{6}$);
(2)(2$\sqrt{18}$-3$\sqrt{32}$)÷$\sqrt{6}$;
(3)(5$\sqrt{3}$-2$\sqrt{5}$)2.
分析 (1)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算;
(2)根据二次根式的除法法则运算;
(3)利用完全平方公式计算.
解答 解:(1)原式=($\sqrt{6}$-$\frac{\sqrt{6}}{6}$-$\sqrt{6}$)×(-2$\sqrt{6}$)
=-$\frac{\sqrt{6}}{6}$×(-2$\sqrt{6}$)
=2;
(2)原式=2$\sqrt{18÷6}$-3$\sqrt{32÷6}$
=2$\sqrt{3}$-4$\sqrt{3}$
=-$\sqrt{3}$;
(3)原式=75-20$\sqrt{15}$+20
=95-20$\sqrt{15}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
16.如果点P(-4,y)在第二象限,则y的取值范围是( )
| A. | y>0 | B. | y<0 | C. | y≥0 | D. | y≤0 |
14.函数y=$\frac{1}{x-3}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x<3 | C. | x=3 | D. | x≠3 |
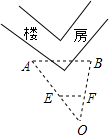 如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.
如图,为了测量有障碍物相隔的A、B两点间的距离,请你通过构造位似图形,设计一种测量方案,需要测量的数据用a,b,c,…表示,并求出A、B间的距离.