题目内容
20．先化简，再求值：（a+1-$\frac{4a-5}{a-1}$）÷（$\frac{1}{a-1}$-$\frac{2}{{a}^{2}-a}$），其中a=1．分析 先计算括号内的部分，再将除法转化为乘法，约分即可．
解答 解：原式=（$\frac{{a}^{2}-1}{a-1}$-$\frac{4a-5}{a-1}$）÷[$\frac{1}{a-1}$-$\frac{2}{a（a-1）}$]
=$\frac{{a}^{2}-4a+4}{a-1}$÷$\frac{a-2}{a（a-1）}$
=$\frac{（a-2）^{2}}{a-1}$•$\frac{a（a-1）}{a-2}$
=a（a-2）
=a2-2a，
当a=1时，原式=1-2=-1．
点评 本题考查了分式的化简求值，熟悉分式的加减和因式分解是解题的关键．
练习册系列答案
相关题目
如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次交换，如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（-2012，2）．．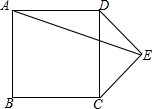
如图，在正方形ABCD外作等腰直角△CDE，DE=CE，连接AE，则sin∠AED=$\frac{\sqrt{5}}{5}$．