题目内容
15.(1)$\sqrt{12}-{({\frac{{\sqrt{3}}}{3}})^{-1}}+\sqrt{3}({\sqrt{3}-1})-{2013^0}-|{\sqrt{3}-2}|$(2)$(2\sqrt{6}-\sqrt{3}+\sqrt{2})×(2\sqrt{6}-\sqrt{3}-\sqrt{2})$.
分析 (1)根据绝对值、零指数幂和负整数整数幂的意义得到原式=2$\sqrt{3}$-$\sqrt{3}$+3-$\sqrt{3}$-1+$\sqrt{3}$-2,然后合并即可;
(2)先根据平方差公式得到原式=(2$\sqrt{6}$-$\sqrt{3}$)2-($\sqrt{2}$)2,然后利用完全平方公式计算.
解答 解:(1)原式=2$\sqrt{3}$-$\sqrt{3}$+3-$\sqrt{3}$-1+$\sqrt{3}$-2
=$\sqrt{3}$;
(2)原式=[(2$\sqrt{6}$-$\sqrt{3}$)+$\sqrt{2}$][(2$\sqrt{6}$-$\sqrt{3}$)-$\sqrt{2}$]
=(2$\sqrt{6}$-$\sqrt{3}$)2-($\sqrt{2}$)2
=24-12$\sqrt{2}$+3-2
=25-12$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂与负整数整数幂.

练习册系列答案
相关题目
10.下列命题错误的是( )
| A. | 两个角的余角相等,则这两个角相等 | |
| B. | 两条平行线被第三条直线所截内错角的平分线平行 | |
| C. | 无理数包括正无理数,0,负无理数 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
7.若代数式$\frac{{\sqrt{5x-3}}}{5}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{3}{5}$ | B. | x<$\frac{3}{5}$ | C. | x≥$\frac{3}{5}$ | D. | x≤$\frac{3}{5}$ |
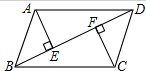 如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.