题目内容
4.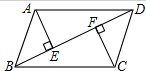 如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
分析 根据平行四边形的性质得出AB=CD,AB∥CD,根据平行线的性质得出∠ABE=∠CDF,求出∠AEB=∠CFD=90°,根据AAS推出△ABE≌△CDF即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠AEB=∠CFD}\\{∠ABE=∠CDF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AE=CF.
点评 本题考查了平行四边形的性质,平行线的性质,全等三角形的性质和判定的应用,解此题的关键是求出△ABE≌△CDF,注意:平行四边形的对边平行且相等,难度适中.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.已知空气的单位体积质量为0.00124克/厘米3,将0.00124这个数用科学记数法表示为( )
| A. | 0.124×10-2 | B. | 1.24×10-3 | C. | 1.24×103 | D. | 1.24×102 |
16.函数$y=\frac{x}{{\sqrt{3-2x}}}$中,自变量x的取值范围是( )
| A. | $x<\frac{2}{3}$ | B. | $x<\frac{3}{2}$ | C. | $x≥\frac{2}{3}$ | D. | $x≥\frac{3}{2}$ |
 如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.
如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.