题目内容
7.已知$\frac{1}{x}$-$\frac{1}{y}$=4,xy=-1,则$\frac{1}{{x}^{4}}$-$\frac{1}{{y}^{4}}$=112$\sqrt{3}$.分析 先根据分式混合运算的法则把原式进行化简,再根据$\frac{1}{x}$-$\frac{1}{y}$=4,xy=-1求出$\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$=14,$\frac{1}{x}$+$\frac{1}{y}$=2$\sqrt{3}$,代入原式进行计算即可.
解答 解:∵$\frac{1}{x}$-$\frac{1}{y}$=4,xy=-1,
∴($\frac{1}{x}$-$\frac{1}{y}$)2=16,
∴$\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$=16-2=14,$\frac{1}{x}$+$\frac{1}{y}$=$\sqrt{{(\frac{1}{x}-\frac{1}{y})}^{2}+\frac{4}{xy}}$=$\sqrt{16-4}$=2$\sqrt{3}$,
∴原式=($\frac{1}{{x}^{2}}$-$\frac{1}{{y}^{2}}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)
=($\frac{1}{x}$+$\frac{1}{y}$)($\frac{1}{x}$-$\frac{1}{y}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)
=2$\sqrt{3}$×4×14
=112$\sqrt{3}$.
故答案为:112$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
17.这些图形中,既是轴对称图形,又是中心对称轴图形的是( )
| A. |  | B. |  | C. |  | D. |  |
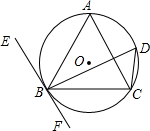 如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=$\sqrt{3}$cm.
如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=$\sqrt{3}$cm.