题目内容
6.生活中的车轮都是圆的,它主要是利用了圆的特性,这样我们在平地上行驶才会平稳,但是爱玩车模拼装的王小果给他的电动玩具车装的轮子却是正多边形的(车轴过正多边形中心),那它在平路上行驶将会怎样呢?请认真思考,回答下列问题:问题1:以图2中的正方形所在的位置为轮子开始运动的位置,请在图2中画出正方形的中心O和顶点A随该轮子滚动一周(无滑动)的运动路径,若该轮子的边长为20cm,请计算出点A和点O随该轮子滚动一周时所经过的路径长.
问题2:如图3、图4,若轮子是正五边形、正六边形时,请在图3、4中画出中心O随该轮子滚动一周时的运动路径.
问题3:观察图2、3、4,当边长为20cm的正n边形的边数n至少为26时,汽车上下颠簸的幅度不超过1.7cm.
分析 (1)根据题意,画出正方形“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(2)根据题意,画出正五方形和正六边形“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(3)根据正多边形的两顶点最长即为最大幅度计算即可.
解答 解:问题1:画出A点与O点运动的轨迹,如图所示,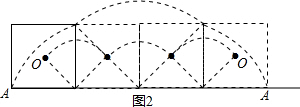
∵轮子的边长为20cm,
∴点A随该轮子滚动一周时所经过的路径长为2×$\frac{90π×20}{180}$+$\frac{90π×20\sqrt{2}}{180}$=(20π+10$\sqrt{2}$π)cm;
点O随该轮子滚动一周时所经过的路径长为3×$\frac{90π×10\sqrt{2}}{180}$=15$\sqrt{2}$π(cm);
问题2:若轮子是正五边形时,在图3中画出中心O随该轮子滚动一周时的运动路径,如图所示: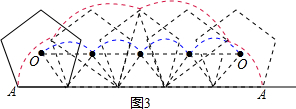
若轮子是正六边形时,在图3中画出中心O随该轮子滚动一周时的运动路径,如图所示: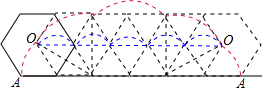
问题3: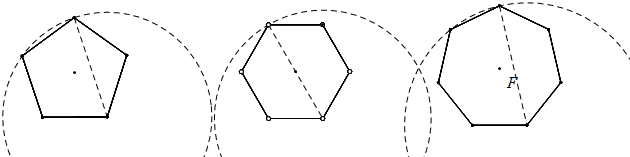
正多边形的两顶点最长即为最大幅度,可得$cosα=\frac{\frac{1}{2}×20}{\frac{1}{2}×1.7×100}$,
解得:α=83°,
所以可得内角为166°,
故边数为:360°÷(180°-166°)≈26.
故答案为:26.
点评 本题考查了弧长的计算、正方形的性质.在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°.

练习册系列答案
相关题目
16.函数$y=\frac{x}{{\sqrt{3-2x}}}$中,自变量x的取值范围是( )
| A. | $x<\frac{2}{3}$ | B. | $x<\frac{3}{2}$ | C. | $x≥\frac{2}{3}$ | D. | $x≥\frac{3}{2}$ |

 设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证:
设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证: