题目内容
17.在平面直角坐标系中,有一个长方形ABCD,AB=4,BC=3且AB∥x轴,BC∥y轴,把这个长方形首先向左平移7个单位,再向上平移5个单位,然后沿着y轴翻折得长方形A1B1C1D1,在这个过程中A与A1,B与B1,C与C1,D与D1分别表示始末位置长方形中相同位置的顶点,已知A1坐标是(5,1),那么A点坐标是( )| A. | (2,-4) | B. | (6,-4) | C. | (6,-1) | D. | (2,-1) |
分析 首先根据关于y轴对称的坐标特点可得沿着y轴翻折前的坐标为(-5,1),再根据平移方法可得A点坐标是(-5+7,1-5),进而可得答案.
解答 解:∵A1坐标是(5,1),
∴沿着y轴翻折前的坐标为(-5,1),
∵把这个长方形首先向左平移7个单位,再向上平移5个单位得到A的对应点(-5,1),
∴A点坐标是(-5+7,1-5),
即(2,-4),
故选:A.
点评 此题主要考查了坐标与图形的变化--平移,以及关于y轴对称的坐标特点,关键是正确理解题意,掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.下列各式表示正确的是( )
| A. | $\sqrt{9}$=±3 | B. | ±$\sqrt{9}$=3 | C. | $±\sqrt{9}$=±3 | D. | ±$\sqrt{(-3)^{2}}$=-3 |
7.方程x2-6x+9=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).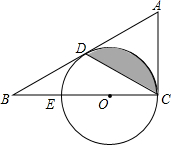 如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.
如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.