题目内容
5．在梯形ABCD中，AB∥CD，AC与BD相交于点O，且DC=$\frac{1}{2}$AB，则S△ODC：S△OBA=1：4．分析 由AB∥CD，得到△ODC∽△OBA，根据相似三角形的性质即可得到结论．
解答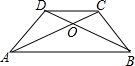 
解：∵AB∥CD，
∴△ODC∽△OBA，
∴S△ODC：S△AOB=DC2：AB2=1：4．
故答案为：1：4．
点评 本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其它两边所截的三角形与原三角形相似；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
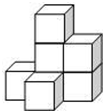如图，若干个小正方体组成一个几何体．
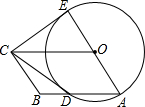如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交⊙O于E，连接CD，CE，若CE是⊙O的切线，
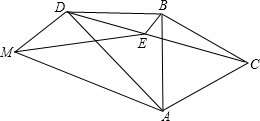如图，四边形ABDM中，AB=BD，AB⊥BD，∠AMD=60°，以AB为边作等边△ABC，∠ABD的平分线BE交CD于点E，连接ME．
如图，将边长为8的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，求：
综合平面直角坐标系，探讨：