题目内容
18.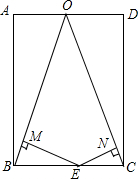 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.
分析 过B作BH⊥OC于H,过E作EM⊥BH于M,由四边形EGHN是矩形,得到EN=HM,根据矩形的性质得到∠A=∠D=90°,AB=CD,证得△ABO≌△CDO,得到OB=OC,推出△BEM≌△BEG,得到BG=EM,等量代换得到BH=EM+EN,由△BCH∽△CDO,得到比例式,即可得到结论.
解答 解:过B作BH⊥OC于H,过E作EG⊥BH于G,
则四边形EGHN是矩形,
∴EN=HM,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD,
∵O是AD的中点,
∴AO=DO,
在△ABO与△CDO中,
$\left\{\begin{array}{l}{AB=CD}\\{∠A=∠D}\\{AO=DO}\end{array}\right.$,
∴△ABO≌△CDO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠GEB=∠OCB,
在△BEM与△BGE中,
$\left\{\begin{array}{l}{∠BME=∠EGB}\\{∠MBE=∠GEB}\\{BE=BE}\end{array}\right.$,
∴△BEM≌△BEG,
∴BG=EM,
∴BH=EM+EN,
∵AD∥BC,
∴∠DOC=∠OCB,
∵∠D=∠BHC=90°,
∴△BCH∽△CDO,
∴$\frac{CD}{BH}=\frac{OC}{BC}$,
∵OC=$\sqrt{O{D}^{2}+C{D}^{2}}$=$\sqrt{10}$,
∴BH=$\frac{3\sqrt{10}}{5}$,
∴EM+EN的值为:$\frac{3\sqrt{10}}{5}$.
点评 本题考查了矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )
有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )
 有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )
有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )| A. | x(9-x)米2 | B. | x(18-2x)米2 | C. | x(9-3x)米2 | D. | $x(9-\frac{3}{2}x)$米2 |
6.下列根式中,是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{7}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | $\sqrt{\frac{1}{2}}$ |
3.下列命题不是真命题的是( )
| A. | 等腰梯形对角线相等 | |
| B. | 一组对边平行另一组对边相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
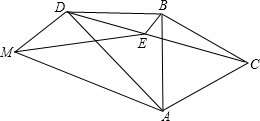 如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.
如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.