题目内容
15.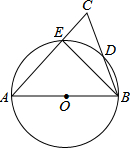 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
分析 连结AD,如图,根据圆周角定理得∠ADB=90°,加上CD=BD,则可判断△ABC为等腰三角形,于是可对(2)进行判断;由于∠ABC=∠C=70°,则∠BAC=40°,则可对(1)进行判断,加上∠AEB=90°,所以∠ABE=50°,则可对(3)进行判断;连结ED,如图,证明△CED∽△CBA,利用相似比可对(4)进行判断.
解答 解:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,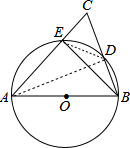
∴AD⊥BC,
而CD=BD,
∴△ABC为等腰三角形,
∴AC=AB,所以(2)正确.
∠ABC=∠C=70°,
∴∠BAC=180°-2×70°=40°,所以(1)错误,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠ABE=50°,
∴AE>BE,所以(3)错误;
连结ED,如图,
∵∠CED=∠ABC,∠ECD=∠BCA,
∴△CED∽△CBA,
∴$\frac{CE}{CB}$=$\frac{CD}{CA}$,
即CE•CA=CD•CB,
∵CA=AB,BD=CD,
∴CE•AB=2BD2,所以(4)正确.
故答案为(2)、(4).
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和相似三角形的判定与性质.

练习册系列答案
相关题目
6.下列根式中,是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{7}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | $\sqrt{\frac{1}{2}}$ |
3.下列命题不是真命题的是( )
| A. | 等腰梯形对角线相等 | |
| B. | 一组对边平行另一组对边相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
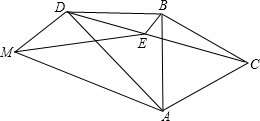 如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.
如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.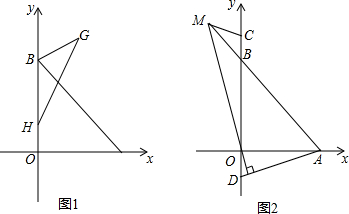
 已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.
已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.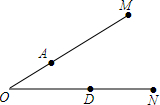 如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.